設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交系。
基本介紹
- 中文名:規範正交系
- 外文名:Normative orthogonal system
- 領域:數學
- 屬性:範數都為1的正交系
- 範疇:正交系
- 相關名詞:規範正交基
簡介

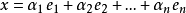


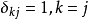

基本性質







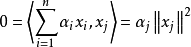

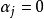

套用
在傅立葉係數



在Bessel不等式

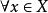
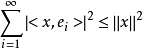
在級數


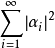
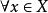

舉例


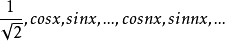

設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交系。

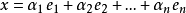


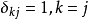








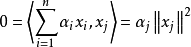

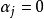





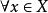
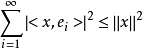


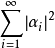
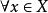



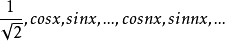

設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交系。...
規範正交基(orthonormal basis)完備的規範正交系。設H為希爾伯特空間,H的完備的規範正交系F稱為H的規範正交基或正規正交基。F的基數稱為希爾伯特空間H的維數。兩...
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。...... 正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域...
正交化是指將線性無關向量系轉化為正交系的過程。設{xn}是內積空間H中有限個或可列個線性無關的向量,則必定有H中的規範正交系{en}使得對每個正整數n(當{xn...
沃爾什正交系是拉德瑪赫爾函式系的完備化,是由美國數學家沃爾什於1923年建立的。...... 沃爾什正交系是由美國數學家沃爾什於1923年建立的,它不僅在 [0,1] 上是...
把線性無關向量系進行正交化的過程,稱為格拉姆-施密特正交化過程。...... 向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交...
對於希爾伯特空間H的規範正交系{ek},如果包含{ek}的最小閉子空間就是H,就稱{ek}為H的完備規範正交系。設{ek}是規範正交系,則H中任一向量 x在ek方向的投影...
的規範正交多項式系;是首項係數為1的n次代數多項式,而且埃爾米特多項式系定義 常稱 為埃爾米特多項式系,而稱Hn(x)為n階埃爾米特多項式。它在[0,+∞)內有n個...
f u,. fix) f…是與這些特徵值對應的所有特徵函式組成的規範正交系.其次,設h(x)EIZ[a,h],如果積分此級數在「Qe司上絕對且一致收斂.[1] 參考資料 1. ...
