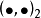C2類運算元稱為希爾伯特-施密特運算元,而相應的範數‖·‖2稱為希爾伯特-施密特範數。
基本介紹
- 中文名:希爾伯特-施密特運算元
- 外文名:Hilbert-Schmidt operator
- 適用範圍:數理科學
簡介,施凱特p類運算元,定義,性質,
簡介
施凱特p類運算元
施凱特 p 類運算元是緊運算元中重要的子類。
設H是可分的希爾伯特空間,𝓚(H)是H上的緊運算元全體,對於 T 𝓚(H)
𝓚(H)



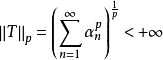
定義
若 ,則
,則 。當 1≤p<q,則
。當 1≤p<q,則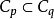 。若p,q,r滿足
。若p,q,r滿足


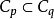


特別重要的是p=1,2的情形。C1和C2類運算元分別稱為跡類運算元和希爾伯特-施密特運算元,而相應的範數‖·‖1和‖·‖2分別稱為跡範數和希爾伯特-施密特範數。
性質
設{en}是H的規範正交基,當T∈C1時,T的跡tr(T)定義為

當 時,
時,