基本介紹
- 中文名:對稱核線性積分運算元
- 外文名:linear integral operator with symmetric kernel
- 所屬學科:數學(泛函分析)
- 所屬問題:泛函分析(微分運算元與積分運算元)
- 別稱:具有埃爾米特核的線性積分運算元
- 相關人物:希爾伯特和施密特等
定義





特徵值與特徵函式


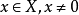

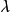

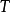
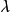

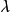






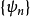

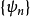

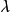

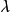
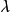


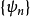

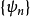
希爾伯特-施密特定理


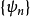

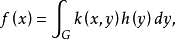
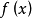
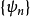

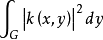
希爾伯特-施密特積分運算元
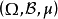






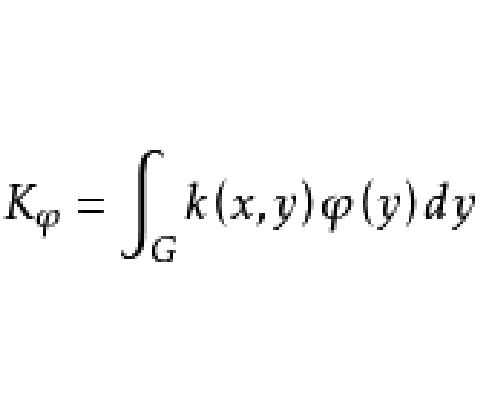







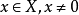

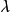

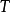
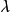

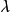






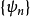

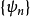


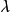
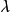


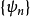

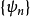


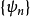

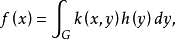
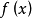
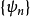

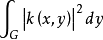






對稱核線性積分運算元(linear integral operator with symmetric kernel)是具有對稱核的線性積分運算元,又稱為具有埃爾米特核的線性積分運算元。對稱核線性積分運算元理論,是...
對稱核線性積分運算元特徵值是矩陣特徵值概念的推廣。對於具有對稱核k(x,y)的線性積分運算元,如果k在G×G上是平方可積的,並且不恆等於0,那么K的特徵值與特徵函式...
例如,對泛函分析中平方可積函式、平均收斂、運算元等的形成,對一般線性運算元理論的...特別是關於對稱核積分方程的特徵值存在性,對稱核關於特徵函式序列的展開,以及...
線性積分運算元分解是運算元的一種分解。所謂線性積分運算元的分解,是指把一個線性積分運算元分解為另外兩個或幾個線性運算元的複合。這種分解,在許多問題中是有重要意義的。...
真是積分運算元 的最小特徵值,則方程(3)在 中至少有一解。定理2 設核 為連續實對稱正核, 連續,並且存在 及 ( 同上),使則(3)在 中至少有一解。定理3 如...
弗雷德霍姆線性積分運算元是一類重要的線性積分運算元,是n維空間上的線性運算元當n變成無窮時的極限式。...
線性積分運算元全連續性(complete continu-ity of linear integral operator)全連續性是線性積分運算元特有的基本性質.設k<x,婦是GXG上的平方可積函式,則以k(二,y)...
解和對稱核相關的理論;③與經典的弗雷德霍姆定理 不成立的線性積分方程的問題;...自抽象空間這個概念創立以來,如希爾伯特空間、巴拿赫空間以及運算元理論的建立,使古典...
的解析方法和數值方法,其中涉及的積分核有連續核、平方可積核、對稱核、卷積核...2.5 線性運算元2.6 線性運算元的譜習題3 連續或平方可積核積分方程...
如果像f在每個點x處的值f(x)由原像u和它的某些導函式在x處的值所決定,則稱A為微分運算元。當A還是線性時,稱A是線性微分運算元。...
沃爾泰拉線性積分運算元是一類重要的線性積分運算元,沃爾泰拉(Volterra,V.)於1896-1897年首先系統地研究了這一類運算元。...
運算元高階導數的概念要求引入多線性運算元,實際上,高階 F導數還是對稱的多線性運算元。帶餘項的泰勒公式在形式上與函式的泰勒公式是一樣的。...
正定核是一類特殊的對稱核,其相應的線性積分運算元的特徵值都是正的。若 K 僅有有限多個負特徵值,則稱 k(x,y) 必是擬正定核。...
設對稱核 k(x,y) 是G×G上的平方可積函式, K是以k(x,y)為核的線性積分運算元。若K僅有有限多個負特徵值,則稱k(x,y)必是擬正定核。...
希爾伯特-施密特定理是對稱核線性積分運算元的基本定理,是希爾伯特(Hilbert,D.)和施密特(Schmidt,E.)所建立的。這一定理在對稱核線性積分方程理論中起重要作用。...
(K′稱為K的轉置核),若K′=K,則稱K為對稱核;當Ω為阿貝爾群且有K(x,y...設k(x,y)是線性積分運算元的核,令k1(x,y)=k(x,y),用歸納法定義:...
6.2 自共軛運算元的譜 1686.2.1 有界自共軛運算元譜的性質 1686.2.2 全連續自共軛線性運算元的特徵展開 1716.2.3 具有對稱核的積分方程 176習題六 179第七章...
