基本介紹
- 中文名:非線性積分方程
- 外文名:nonlinear integral equation
- 所屬學科:數學
- 所屬問題:積分方程(非線性積分方程)
- 舉例:弗雷德霍姆型、沃爾泰拉型等
基本介紹




Fredholm型非線性積分方程



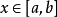

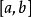


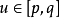
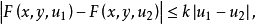



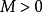

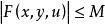
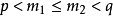
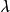


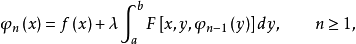
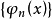
Volterra型非線性積分方程

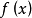


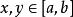

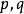
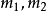
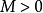

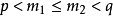


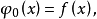

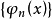
Hammertein型非線性積分方程

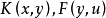





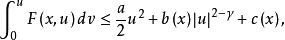











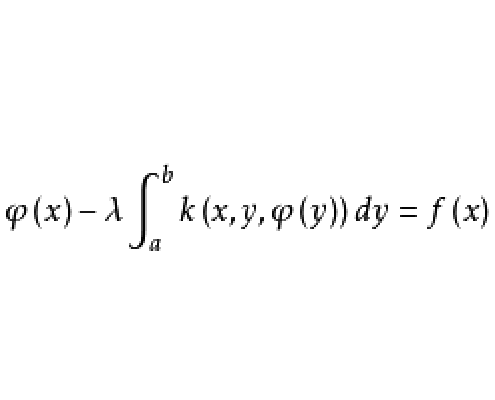







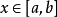

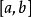


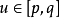
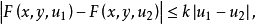



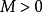

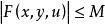
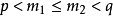
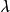


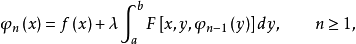
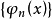

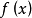


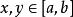

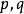
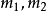
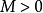

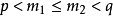


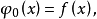

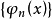

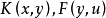





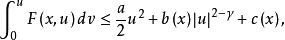











非線性積分方程(nonlinear integral equation)是指不具有線性性質的一類積分方程。如果未知函式在積分號下是以非線性形式出現的,這種方程就稱為非線性積分方程。非線性...
《線性與非線性積分方程:方法及套用》是一本2011年高等教育出版社出版的圖書,作者是佤斯瓦茨。...
積分號下含有未知函式的方程。其中未知函式以線性形式出現的,稱為線性積分方程;否則稱為非線性積分方程。積分方程起源於物理問題。牛頓第二運動定律的出現,促進了微分...
《積分方程(第3版)》是2012年由沈以淡編著,清華大學出版社出版的一本書籍。...... 方程、積分方程的數值解法,此外對奇異積分方程、積分方程組及非線性積分方程等...
線性積分方程(linear integral equation)是積分方程的主要研究對象,若方程中未知函式包含在積分號下,這個方程稱為積分方程。當積分方程中的未知函式是一次時,就稱為...
如果把非線性積分方程中出現的函式看做巴拿赫空間中的元素,那么原來的積分運算就將構成一個非線性積分運算元 T 。常見的非線性積分運算元有:烏雷松運算元、沃爾泰拉運算元、...
非線性沃爾泰拉積分方程(nonlinear Volterraintegral equation)積分上限變動的一類特殊的非線性方程.這指的是如下方程 這時,對任意幾,方程(1)在z,`La,b}內都存在...
非線性弗雷德霍姆積分方程(nonlinear Fred-holm integral equation)一類特殊的非線性積分方程.這指的是方程 這時,對ICI<1/N,方程(1)在z,2 Ca } b]內一定存在...
非線性方程,就是因變數與自變數之間的關係不是線性的關係,這類方程很多,例如平方關係、對數關係、指數關係、三角函式關係等等。求解此類方程往往很難得到精確解,經常...
考慮到泛函分析與積分方程的密切關係,增加了對泛函分析基本知識的介紹。出於篇幅的考慮,本書沒有涉及Cauchy型奇異積分方程和非線性積分方程。本書適合作為高等院校數學...
《高等學校數學系列教材·積分方程論(修訂版)》重點是線性Fredholm第二種方程,但對第一種方程,Volterra方程、非線性方程、卷積型方程、核密度為Lz的Cauchy型奇異積分...
哈默斯坦方程(Hammerstein equation)是一類重要的非線性積分方程。...... 哈默斯坦方程(Hammerstein equation)是一類重要的非線性積分方程。它指的是如下形式的積分方程:...
這種分解,在許多問題中是有重要意義的。例如,在利用變分方法研究非線性積分方程解的性質時,線性積分運算元的分解起著重要作用。線性積分運算元分解性質 編輯 ...
《非線性泛函分析》是2015年高等教育出版社出版的圖書,作者是郭大鈞。...... 第三章將半序和拓撲度(不動點指數)相結合來研究非線性運算元方程的正解,討論了常用的...
烏雷松非線性積分運算元是一類相當廣泛的非線性積分運算元。這類運算元是由烏雷松於1924年首先提出並加以研究的。...
《非線性偏微分方程近代分析方法》研究生教材,該書大部分內容取自我們指導的博士發表的論文和研究成果,內容包括微分方程相似變換理論、函式分析理論、積分方程理論、...
《線性與非線性積分方程:方法及套用》是2011年6月1日高等教育出版社出版的圖書,作者是(美國)佤斯瓦茨(Abdul-Majid Wazwaz)。...
玻耳茲曼方程正文 氣體分子運動論的基本方程,因L. E. 玻耳茲曼於1872年首先提出而得名。它是一個非線性積分微分方程,用於描述氣體分子速度分布函式的變化。它對研究...
此外,還可以將方程分為線性方程和非線性方程。方程式自然科學中的方程式 編輯 在自然科學中,通常用一類特殊的式子,用來表示微觀粒子間在特定條件下相互轉化的過程,...
構造近似的等價序列將其轉化為一組線性非齊次兩點邊值問題序列,通過疊代求解一系列的向量微分方程,包括狀態向量方程序列和共態向量方程序列,得到原非線性系統近似最優...
《偏微分-積分方程的有限元方法》是2009年科學出版社出版的書籍,作者是張鐵。...... 主要內容有:半離散和全離散有限元逼近及其在各種範數下的誤差分析,非線性問題...
一階非線性偏微分方程(non-linear partial dif- ferential equation of first order)一階的完全非線 J勝偏微分方程.兩個自變數的一階非線性偏微分方 程的一般...
《非線性玻耳茲曼方程》是2011年科學出版社出版的圖書,作者是張顯文。本書介紹了非線性玻耳茲曼方程的基本知識和一些重要進展。...
1981年在北京核物理講習班上,可以套用吳式樞教授提出的非線性積分方程理論解決“關於π凝聚問題”的一個尚未解決的難題,他當即被邀請去聯邦德國講學與工作,並作為...
5、 《含非線性參數ypbjooh方程的支點》 《數學進展》:3(1964),37—406、 《關於一類非線性Volter型積分方程》《數學學報》14:5(1964)735—7467、 《非...
馬季歐積分方程的核,貝塞爾函式的級數展開以及核的分解,豫解核的基本性質等做了廣泛的研究.在他的指導下,他的學生線上性、非線性積分方程和奇異積分方程等方面繼續...
著有《非線性泛函分析》,合編《數學分析》、《實變函式與泛函分析》、《非線性積分方程》等。 郭大鈞(Guo Dajun)(1934.1.23—— )誕生於四川瀘縣。山東大學...
