彼得-外爾定理

彼得-外爾定理指的是經典三角多項式可一致逼近連續函式的定理在緊李群上的一種推廣。

基本介紹

• 中文名：彼得-外爾定理
• 外文名：Peter-Weyl theorem
• 適用範圍：數理科學

簡介

彼得-外爾定理指的是經典三角多項式可一致逼近連續函式的定理在緊李群上的一種推廣。

在經典的傅立葉級數理論中，一個熟知的結果是，任一以2π為周期的連續函式可用三角多項式來一致逼近，這一經典結果在緊李群上的推廣，即是著名的彼得-外爾定理。

具體內容

設G是一個緊李群，則G的不可約表示必是有限維的，且G的有限維表示必等價於一個酉表示。所以，在表示空間中取一組適當的規範正交基時，G的不可約表示將G的元映成酉矩陣。設{U_λ|λ∈Ĝ}是緊李群G的不可約酉表示完全組，則U_λ(x)的每個矩陣係數定義了G上的實解析函式。相應於L²(G)的內積，U_λ(x)的不同矩陣係數彼此正交；當λ₁,λ₂∈Ĝ且λ₁≠λ₂時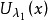，與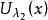的不同矩陣係數也彼此正交。這時彼得-外爾定理可敘述為：緊李群G的不可約酉表示完全組{U_λ|λ∈Ĝ}的矩陣係數全體是L²(G)的完備正交函式系，G上的任一連續函式可用該正交系中函式的有限線性組合來一致逼近。

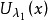
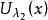
上述緊李群G的完備正交函式系在緊李群上調和分析中的地位，等同於{e^inx|n=0,±1,...}在經典傅立葉分析中的地位。

緊李群

(compact Lie group)

緊李群是拓撲結構為緊的李群。

設G為李群，作為流形它有拓撲結構，若這個拓撲為緊拓撲，則G稱為緊李群。

緊李群只有有限多個連通分支，緊李群的李代數為緊李代數，且連通李群緊若且唯若它的李代數為緊李代數。復緊李群必可交換，它就是復環面。