德國數學家。1885年11月9日生於德國漢堡附近的埃爾姆斯霍恩,1955年12月8日因心臟病突發在蘇黎世去世。他1904年入哥廷根大學,1905~1906年在慕尼黑大學學習數學、物理、化學。1907年在D.希爾伯特的指導下,完成博士論文《奇異積分方程,特別考慮傅立葉積分定理》,1908年獲博士學位。1910年獲無薪講師資格。
1913年受聘任瑞士蘇黎世的聯邦工學院教授,同A.愛因斯坦結下友誼。1930年回哥廷根繼承希爾伯特的教授席位,1933年任哥廷根數學研究所所長。同年夏天,應新成立的美國普林斯頓高等研究所之聘任該所教授,1951年退休。
正文
外爾是20世紀上半葉最重要的數學家之一。他的早期工作(1908~1915)是在分析學方面。其博士論文中把希爾伯特及其學生關於積分方程的工作推廣到積分上限為無窮的情形。其後研究奇異特徵值問題,把經典的斯圖姆-劉維爾方程從有限區間推廣到無窮情形。他還研究特徵值取虛數值的情形。1911年起,他研究振動物體的特徵頻率的漸進分布,開創了特徵值漸近展開理論。
外爾的重要著作《黎曼曲面的思想》(1913)第一次給黎曼曲面奠定了嚴格的拓撲基礎。他運用希爾伯特提出的鄰域概念把曲面定義為可三角剖分的連通點集。這些思想,可以說是後來拓撲空間和複流形理論的先聲。他還引進一些閉鏈和上鏈等概念,預示著代數拓撲學的發展。大約同時,外爾轉向實數(тod 1)的一致分布問題,證明了基本定理(1914):一實數列α,α,…,α,按(тod1)是一致分布的,若且唯若→∞時,對於任何非零整數,有。他還得出指數和估計的外爾不等式。這導致一系列解析數論問題的改進。
1915~1933年,他研究與物理有關的數學問題。他企圖解決引力場與電磁場的統一理論問題。他把電磁勢納入幾何框架,由此得出規範變換和規範不變性的概念。雖然,他企圖統一場論的第一次嘗試沒有成功,但對以後發展起來的各種場理論和廣義微分幾何學有深遠影響。他的幾何工作直接導致一般微分幾何學特別是聯絡和纖維叢等概念的發展。20年代初,他從一般空間問題進而研究連續群的表示,導致他1925~1927年最出色的工作,其中包括運用大範圍方法研究半單純李群的線性表示,以及緊群的彼得-外爾定理。他把經典的有限群結果擴張到緊群上去,又通過“酉技巧”擴張到非緊的半單群上。他引進的外爾群是數學中的重要工具,而且能對許多具體的群得出具體的結果。量子力學產生之後,他首先把群論套用到量子力學中,著有《群論與量子力學》(1928),並套用群論解決一系列物理、化學問題。其後,他把不變式論與群表示論結合起來,總結在《典型群》(1939)一書中。
在蘇黎世期間,外爾對哲學和數學基礎的觀點產生了變化。在哥廷根時他曾受到希爾伯特形式主義觀點的影響,這時他贊同L.E.J.布勞威爾的直覺主義,反對非構造性的存在證明,反對G.(F.P.)康托爾的超窮數,說那些是“霧中之霧”。外爾和希爾伯特儘管有對立的數學哲學觀點,但仍保持著良好的師生情誼。希爾伯特退休時,外爾成為他的繼承人。
外爾到普林斯頓後的工作大都是以前工作的繼續。其間有研究凸多面體的剛性和變形問題(1916~1917,1935)、維旋量、黎曼矩陣、平均運動(1938~1939)、數的幾何、推廣奈望林納亞純函式理論到亞純曲線(1938),邊界層問題(1942)等等。外爾的論文收在《外爾全集》(共4卷,1968)中。
 外爾,(C.H.)H.
外爾,(C.H.)H.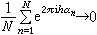 外爾,(C.H.)H.
外爾,(C.H.)H. 外爾,(C.H.)H.
外爾,(C.H.)H.