廣義除數問題

廣義除數問題(generalized divisor problem)是數論中的重要問題。數論是研究數的性質和規律的一門學科。是數學的一個重要分支。對於數學的許多分支學科(例如函式論、幾何、代數、機率論、計算數學、組合數學等)以及套用學科(例如通信技術、密碼學等)的發展有著深刻的影響。

基本介紹

• 中文名：廣義除數問題
• 外文名：generalized divisor problem
• 領域：數學
• 學科：數論
• 性質：數論中的重要問題
• 推廣：除數問題

概念

廣義除數問題是數論中的重要問題。若d_k(n)表示將n表為k個因子乘積的表法種數，又若：

則有：

其中ζ(w)為黎曼ζ函式，w=1為一k次極點，其上的留數形如xP_k(log x)。此外，P_k為一k-1次多項式，記D_k(x)=xP_k(logx)+Δ_k(x)。當k=2時，即為除數問題；當k>2時，即為廣義除數問題。其定義α_k為使Δ_k(x)=O(x)成立的數θ的下極限，估計α_k即為廣義除數問題的中心。對α_k的上界估計，其結果有：

等。一般地，α_k≤(k-1)/(k+2)，k=4，5，…(哈代-李特爾伍德，1992年)，下界估計為α_k≥(k-1)/2k(哈代(Hardy，G.H.)，1915年)，猜想結果是α_k=(k-1)/2k。上列問題，至今仍未解決。

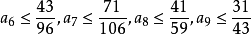
數論

研究數的性質和規律的一門學科。是數學的一個重要分支。對於數學的許多分支學科(例如函式論、幾何、代數、機率論、計算數學、組合數學等)以及套用學科(例如通信技術、密碼學等)的發展有著深刻的影響。其他學科的研究成果和思想方法，也對數論的發展有著重要的作用。數論按其內容和方法大致可分為初等的、解析的、代數的與幾何的四類。

初等數論主要是用算術方法研究有理整數性質，包括整數的整除性、同餘式、素數、原根、不定方程等，它不需要較為深入的分析和代數工具，是數學中古老的分支之一.遠在公元前3世紀，古希臘數學家歐幾里得(Euclid)就證明了素數的個數是無窮的.中國古代的《孫子算經》中給出了解一次同餘式組的算法，即著名的“孫子定理”或稱“中國剩餘定理”.從17世紀到19世紀，法國數學家費馬(Fermat，P.de)、瑞士數學家歐拉(Euler，L.)、法國數學家勒讓德(Legendre，A.M.)、德國數學家高斯(Gauss，C.F.)等人的工作大大發展和豐富了初等數論的內容.另外，對初等數論中某些問題的研究，進一步發展了數學中的新分支.如對不定方程和高次互反律的研究，促進了代數數論和類域論的發展.近幾十年來，初等數論在計算機科學、組合數學、密碼學、信號的數字處理等領域得到廣泛的套用，取得了許多深刻的結果.

解析數論在本質上是利用數學中的解析工具來研究數論問題，主要的方法有復積分法、圓法以及三角和方法.在素數分布問題的研究中，俄羅斯數學家切比雪夫(Чебышев，П.Л.)首先引進了與

密切相關的函式：

並證明了θ(x)~x，ψ(x)~x都等價於素數定理，從而為素數定理的研究做出了重要貢獻。德國數學家黎曼(Riemann，G.F.B.)首先對復變數s的函式：

做了系統和深刻的研究，對素數論與函式論的發展產生了深遠的影響。由於英國數學家哈代(Hardy，G.H.)和李特爾伍德(Littlewood，J.E.)的強有力的方法——圓法，以及維諾格拉多夫(Виноградов，И.М.)所創造的“三角和方法”，使得關於奇數的哥德巴赫猜想獲得了基本解決，並使華林問題關於G(k)的估計得到了極為深刻的結果。中國數學家華羅庚在三角和以及一系列著名數論問題中做出了舉世公認的貢獻。特別是陳景潤關於偶數的哥德巴赫猜想的(1+2)的傑出成果，在國際數學界引起了強烈的反響。另外，塞爾貝格(Selberg，A.)、林尼克(Линник，Ю.В.)、邦別里(Bombieri，E.)以及中國數學家王元、潘承洞等在篩法、零點密度、均值定理等許多方面也做出了重要貢獻。

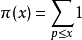
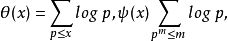
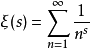
代數數論最初的形成和發展，主要是由於對互反律和費馬大定理等不定方程的研究所推動.目前，代數數論已成為數論中一個內容異常豐富的分支。代數數論研究的主要對象是代數數域，特別是研究一個給定的代數數域中代數整數的算術性質。代數數就是方程a₀x+a₁x+…+a_n-1x+a_n=0的根，其中a₀，a₁，…，a_n-1，a_n都是有理整數.非代數數就稱為“超越數”，近年來關於超越數的深入研究已發展成為數論的一個獨立的分支——超越數論。德國數學家庫默爾(Kummer，E.E.)為了解決費馬大定理，首先創立了理想數理論，為代數數論奠定了基礎。德國數學家戴德金(Dedekind，J.W.R.)系統地發展了庫默爾理論，建立了代數數論的基本理論，主要是代數數域的整數環的結構、素理想分解、單位群、理想類群性質等. 亨澤爾(Hensel，K.)開創的p-adic數理論，將賦值論和局部域的研究方法引入代數數論，並最終導致伊代爾和阿代爾概念的引入。19世紀末，由德國數學家希爾伯特(Hilbert，D.)開始，至1927年，由日本數學家高木貞治(Takagi，T.)和阿廷(Artin，E.)完成的類域論，是代數數論的最主要理論之一，它將擴域的伽羅瓦群與基域的理想類群(或伊代爾群)聯繫起來。目前，代數數論的研究手段和範圍已大為擴展，包括代數、函式論、算術、代數幾何等各種方法。希爾伯特、克羅內克(Kronecker，L.)在二次域理論，圖埃(Thue，A.)、西格爾(Siegel，C.L.)、羅特(Roth，K.F.)在丟番圖逼近論中以及外爾(Weyl，(C.H.)H.)在指數和與一致分布中的傑出貢獻都發展和豐富了代數數論。中國數學家華羅庚等在代數數論的許多問題中也做出了重要貢獻。在超越數論中，劉維爾(Liouville，J.)、貝克(Baker，A.)、羅特、蓋爾豐德(Гельфонд，А.О.)、施奈德(Schneider，T.)等人的卓越工作早為國際數學界所矚目。還值得一提的是羅特於1955年所著的《對於代數數的有理逼近》確立了有名的圖埃-西格爾-羅特定理，以及貝克在超越數論方面的卓越貢獻分別榮獲了1958年及1970年的國際菲爾茲數學大獎.後來貝克將其研究成果整理成薄薄的128頁的專著《超越數論》，被認為可與高斯的《算術研究》相媲美。

幾何數論是研究一個平面或空間區域中坐標都為整數的點即整點的個數。例如，著名的圓或橢圓內的整點問題，球或橢球內的整點問題，以及除數問題等。高斯和狄利克雷(Dirichlet，P.G.L.)分別在“圓內整點問題”和“除數問題”的研究中做出了開創性的工作。以後華羅庚、維諾格拉多夫、蘭道(Landau，E.G.H.)、哈代(Hardy，G.H.)等也分別得到了許多重要結果。幾何數論與其他重要數論問題，如二次型理論有密切關係。

近幾年，計算數論也在逐漸發展之中。

數論中的一系列重要問題，如素數分布、哥德巴赫猜想、華林問題、除數問題、圓或球內的整點問題等，都是目前正在研究的問題。特別需要指出的是，目前正在蓬勃發展的丟番圖分析、 超越數論越來越引起世界上許多著名數學家的密切關注，它們已成為一個嶄新的數學分支。