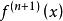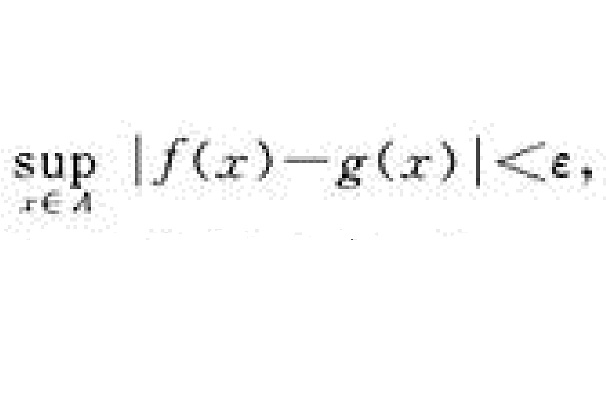一致逼近

一致逼近是無窮級數的基本概念之一，指一類均勻的逼近。

插值方法要求插值函式與被插函式在指定的節點處有相同的函式值及若干階相同的導數．為了提高逼近精度，可以增加插值節點，但增加節點構造的高次插值多項式，往往會產生Runge現象而得不到理想的插值效果．“一致逼近”是要求逼近函式與被逼近函式在整個閉區間上都很接近，可以克服插值逼近的缺陷。

基本介紹

• 中文名：一致逼近
• 外文名：uniform approximation
• 所屬領域：數理科學
• 重點：最佳一致逼近多項式

定義

定義一

如果用函式列f1，f2，…，fn，…逼近函式Φ，取fi與Φ之差的模的上確界

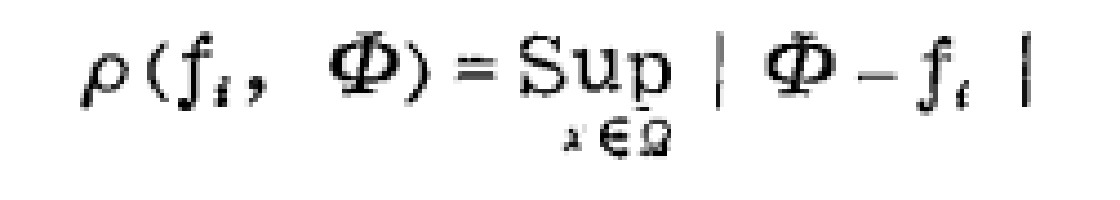
作為fi與Φ的離差之測度，就稱這種逼近是一致逼近，上式中Ω為在其內進行逼近的數集．

若fi(i=1，2，…，n，…)和Φ皆連續，而Ω為緊集，則上確界的符號可改為極大值符號。

定義二

① 對於任意的f(x)∈[a，b]，在範數

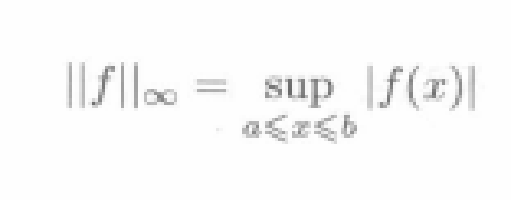
的意義下定義兩個函式的距離：

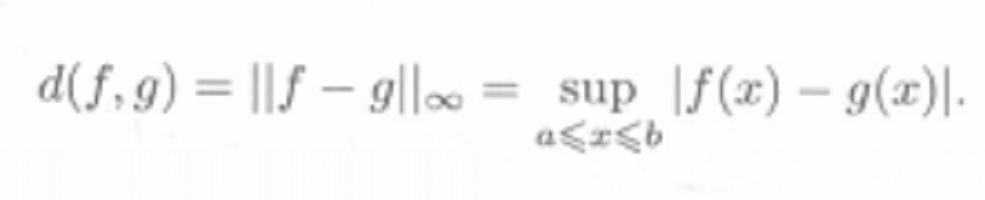
② 若一個函式序列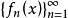 在如上定義的距離的意義下滿足

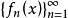
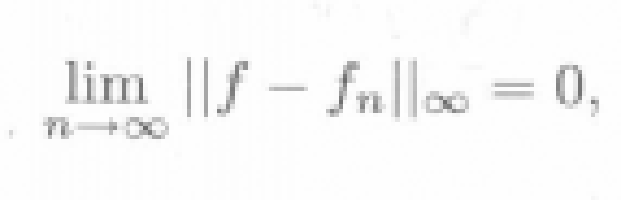
則稱fn(x)在[a，b]上一致收斂於f(x)．

通常也稱在度量||·||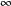 下的逼近問題為一致逼近問題．

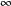
最佳一致逼近

最佳一致逼近多項式

定義 設Pn∈Hn，f(x)∈C[a，b]，稱

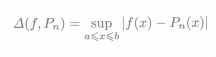
為Pn(X)對於f(x)的偏差，稱

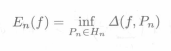
為Pn(x)對f(x)的最小偏差，或稱最佳逼近．

定義 設f(x)∈C[a，b]，若∃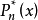 ∈Hn使得

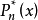
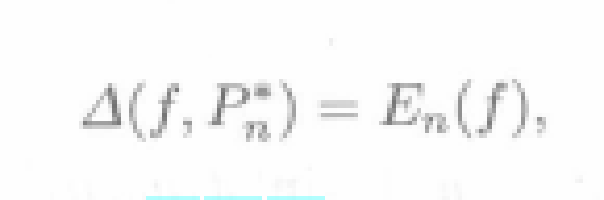
則稱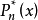 是f(x)在[a，b]上的最佳一致逼近多項式或最小偏差逼近多項式，簡稱最佳逼近多項式．

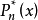
最佳一致逼近多項式的存在性和唯一性

定理1 (Borel，1995)對於任何f(x)∈C[a，b]，在Hn中存在多項式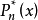 ，使得

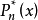
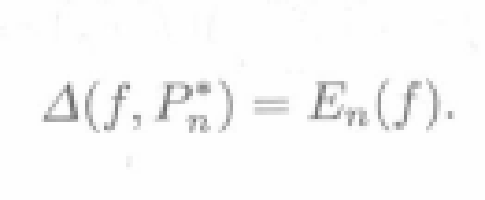
定理2 設f(x)∈C[a，b]，p(x)∈Hn，則p(x)為f(x)的最佳一致逼近多項式的充分必要條件是，f(x)一p(x)在[a，b]上存在一個至少由n+2個點組成的交錯點組。

由該定理可知，若f(x)∈C[a，b]，則在以Hn存在唯一的最佳一致逼近多項式，且最佳一致逼近多項式是f(x)的一個拉格朗日插值多項式。

實際求出最佳一致逼近多項式p(x)往往比較困難。一般利用下述定理求取最佳一致逼近多項式。

定理3 設f(x)在[a，b]上n+1階可導，且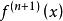 在[a，b]上不變號，若p(x)∈Hn是f(x)的最佳一致逼近多項式，則端點a與b屬於f(x)一p(x)的交錯點組。