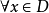函式列(sequence of functions)指各項為具有相同定義域的函式的序列。若{fn}為函式列，其中每個函式fn的定義域為A，則A也稱為{fn}的定義域，若對某個x0∈A，數列{fn(x0)}收斂，則x0稱為{fn}的收斂點，或稱{fn}在點x0收斂，{fn}的所有收斂點的集合稱為它的收斂域。若對每個x∈D，有當n→∞時，fn(x)→f(x)，則函式f(x)稱為函式列{fn}(或{fn(x)})在D上的極限函式，這時也說，函式列{fn}在D上處處收斂於f，或在D上逐點收斂於f。對一般的函式列來說，除研究它的逐點收斂(或稱點態收斂)這種收斂方式外，還要研究一致收斂，這是為了研究極限函式是否繼承相應函式列的各項(函式)所具有的分析性質(連續、可微、可積等)而引入的一種收斂方式。
基本介紹
- 中文名：函式列
- 外文名：sequence of functions
- 所屬學科：數學
- 所屬問題：高等數學（數學分析）
- 簡介：各項具有相同定義域的函式的序列
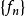
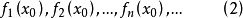
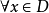
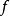
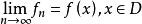
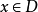
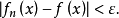
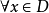
基本概念,函式列的收斂性,函式列的極限函式,函式列的一致收斂性,函式列一致收斂性的定義,函式列一致收斂性的判別,
基本概念
設
函式列的收斂性
設
，將x0代人函式列(1)得到數列：
若數列(2)收斂，則稱函式列(1)在點x0收斂，x0稱為函式列(1)的收斂點。若數列(2)發散，則稱函式列(1)在點x0發散，若函式列(1)在數集
上每一點都收斂，則稱函式列（1）在數集D上收斂，函式列{fn}全體收斂點的集合，稱為函式列{fn}的收斂域。
函式列的極限函式
若函式列(1)在數集D上收斂，這時
，都有數列{
}的一個極限值與之對應，由這個對應法則就確定了D上的一個函式，稱它為函式列{fn}的極限函式，記作
，於是有
函式列極限的ε-N定義：對每一個固定的
，對
（注意：一般說來N值的確定與ε和x的值都有關），使得當n>N時，總有
函式列的一致收斂性
函式列一致收斂性的定義
設{fn}與f定義在數集D上，若 ，當n>N時， ，都有
則稱函式列{fn}在D上一致收斂於f，記作
函式列一致收斂性的判別
(1)柯西準則：{fn}在D上一致收斂
，當n，m>N時， ，都有
(2)餘項準則：
