列維定理

列維定理是實變函式的重要定理。其意義在於對漸升非負可測函式列的極限與取積分號的套用。

基本介紹

• 中文名：列維定理
• 外文名：Levi theorem
• 提出者：列維
• 提出時間：1906年
• 適用領域範圍：數理科學

簡介

列維定理是有關漸升的非負可測函式列積分號下取極限的定理。

這是列維(Levi, B.)於1906年證明的。

定理

設{f_n(x)}是可測集E上非負可測函式列，若：

1、f_n(x)≤f_n+1(x)(n=1,2,...)；

2、幾乎處處收斂於E，則

可測函式

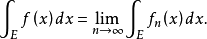
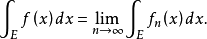
設f是定義在可測集E上的實函式。如果對每一個實數，集E[f>a]恆可測（勒貝格可測），則稱f是定義在 E上的（勒貝格）可測函式。

設(X,F)為一可測空間，E是一個可測集。f: E→R*為定義在E上的函式。若對任意實數a，總有{x∈E: f(x)<a}∈F，則稱f為E上的F-可測函式（簡稱E上的可測函式）。

特別地，若可測空間取為是Rⁿ上的Lebesgue可測空間。E是Rⁿ中的Lebesgue可測集。則E上的可測函式成為Lebesgue可測函式。若可測空間取為Rⁿ上的Borel可測空間，E是Rⁿ中的Borel集，則E上的可測函式稱為Borel可測函式。