阿爾澤拉-阿斯科利定理(阿爾澤拉-阿斯科利定理)

阿爾澤拉﹣阿斯科利(Arzelà–Ascoli)定理是泛函分析中的一個定理，給出了一個從緊緻度量空間射到度量空間的函式集合是否在關於一致收斂的拓撲意義上是緊集的充分必要條件。其中主要涉及的條件是函式集的等度連續性質。

阿爾澤拉-阿斯卡利定理是數學領域的一個基本結果。它是常微分方程組理論中的皮亞諾存在性定理的證明中不可或缺的一環，也是複分析中的蒙泰爾定理的證明中的重要組成部分。此外，它更是調和分析中彼得-外爾定理的證明的關鍵。

基本介紹

• 中文名：阿爾澤拉-阿斯科利定理
• 外文名：Arzelà–Ascoli theorem
• 提出者：阿斯科利，阿爾澤拉
• 提出時間：1895年
• 套用學科：數學

等度連續

定義（分析學）

對於函式列 ,若 ,當 ,有 成立,則稱函式列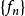 為等度連續的函式列。

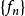
定理

定理一（分析學）：

考慮一定義在閉區間 上的函式序列 ，如果是一致有界，等度連續的，那么函式列 存在一子列 一致收斂。

定理二 （拓撲學）：

X 是一個緊的Hausdorff 空間。那么C(X)的緊緻開拓撲上的一個子集F具有一致範數的充要條件是它是等度連續駐點有界的。

註記

C(X)是X上的所有實連續函式所組成的空間.

一個C(X)的子集F如果是滿足,x存在領域，使得

則稱該子集為等度連續的

一個C(X)的子集F如果是滿足，有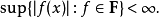則稱稱該子集為駐點有界的.

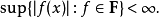
一個C(X)的子集F中的一個元素f的一致範數是指這樣一個非負的範數：