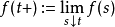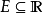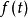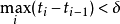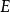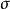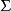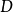基本介紹
- 中文名:右連左極過程
- 外文名:corlol process
- 別稱:右連左極函式
- 領域:數學
定義,例子,累積分布函式,斯科羅霍德空間,斯科羅霍德空間的性質,一致拓撲的一般化,完備性,分離性,斯科羅霍德空間中的胎緊性,代數結構與拓撲結構,
定義
例子
- 全部連續函式都是右連左極函式。
- 由累積分布函式的定義知所有的累積分布函式都是右連左極函式。
累積分布函式
對於所有實數x ,累積分布函式定義如下:

斯科羅霍德空間
從 到
到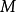 的所有右連左極函式的集合常記為
的所有右連左極函式的集合常記為 或簡記為
或簡記為 ,稱為斯科羅霍德空間,是以烏克蘭數學家阿納托利·斯科羅霍德(Anatoliy Skorokhod)的名字命名。斯科羅霍德空間可以被指派一個拓撲,這一拓撲直覺上能使我們“稍微蠕動空間和時間”(而傳統的一致收斂拓撲僅允許我們“稍微蠕動空間”)。為了簡化說明,取
,稱為斯科羅霍德空間,是以烏克蘭數學家阿納托利·斯科羅霍德(Anatoliy Skorokhod)的名字命名。斯科羅霍德空間可以被指派一個拓撲,這一拓撲直覺上能使我們“稍微蠕動空間和時間”(而傳統的一致收斂拓撲僅允許我們“稍微蠕動空間”)。為了簡化說明,取 ,
,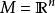 (Billingsley的書中描述了更一般的拓撲)
(Billingsley的書中描述了更一般的拓撲)

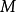



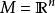
首先我們必須定義連續性模的一個模擬 。對於任意
。對於任意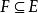 ,使
,使

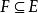

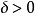


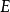


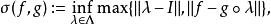

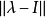

斯科羅霍德空間的性質
一致拓撲的一般化
E上的連續函式空間C是D的一個子空間。相對應於C斯科羅霍德拓撲與這裡所述的一致拓撲相一致。
完備性
雖然D不是關於斯科羅霍德度量σ的一個完備空間,但是可以證明存在具完備性的關於D的拓撲等價度量σ0。
分離性
關於σ或σ0的D是可分空間,因此斯科羅霍德空間是Polish空間。
斯科羅霍德空間中的胎緊性
通過套用阿爾澤拉-阿斯科利定理,我們可以證明斯科羅霍德空間D上機率測度的一個序列 是胎緊的若且唯若同時滿足下列兩個條件:
是胎緊的若且唯若同時滿足下列兩個條件:

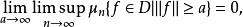

代數結構與拓撲結構
在斯科羅霍德拓撲和函式的逐點加法下,D不是一個拓撲群。