基本介紹
一、定義,1. 下界,2. 下確界,二、常用結論,1. 確界的唯一性定理,2. 確界存在定理,3. 單調有界數列必有極限,
一、定義
1. 下界
設給定一數集E,若存在m R,使得對於
R,使得對於 x
x E,都有x
E,都有x m,則稱m是集合E的一個下界。
m,則稱m是集合E的一個下界。




例:若E= ,不難驗證只要m
,不難驗證只要m
 ,m就是集合E的一個下界。
,m就是集合E的一個下界。



2. 下確界
一個數集可以由有限個數組成,也可以由無窮多個數組成,前者稱為有限(數)集,後者稱為無限(數)集。任何有限數集都有一個最小數,但對於無限數集來說就不一定有最小數了。例如,由一切x 1所組成的數集沒有最小數;又如數集
1所組成的數集沒有最小數;又如數集 (
( )有最小數1/2.
)有最小數1/2.



我們知道,有界數集有無窮多個下界。因而,對於有有界數集來說,如果它有最小數,那么這個最小數也是它的下界中的一個,並且比這個最小數大的任何數都不是它的下界,這時,這個最小數自然就是它的最大的下界。
但在上面的例子中已經看到,對一般無限數集來講不一定有最小數。然而,對於某些無限數集來說,最大的下界確實存在,這裡暫時撇開最大下界的存在性,而對一般數集的最大下界給予確切的定義。
設給定一數集E。若存在這樣一個數 ,適合以下兩個條件:
,適合以下兩個條件:

(i)集E中的一切數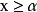 (即
(即 是E的一個下界);
是E的一個下界);
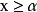

(ii)對任意給定的正數 ,至少存在一個數
,至少存在一個數 ,使得
,使得 (即比
(即比 再大一點就不是下界), 則
再大一點就不是下界), 則 叫做E的下確界,記為
叫做E的下確界,記為 或
或 . 這裡inf是infimum的縮寫。
. 這裡inf是infimum的縮寫。







第一個條件說明 是E的下界之一,而第二個條件說明凡大於
是E的下界之一,而第二個條件說明凡大於 的任何數都不是E的下界。也就是說
的任何數都不是E的下界。也就是說 是E的最大下界。
是E的最大下界。



注1 為方便起見,若E無下界,則記 .
.

注2 上面的條件(ii)等價於:如果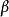 是E的一個下界,則必有
是E的一個下界,則必有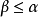 .
.
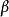
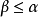
二、常用結論
1. 確界的唯一性定理
定理 設數集有上(下)確界,則這上(下)確界是唯一的。
證明:採用反證法。假設數集E有兩個不同下確界 和
和 (
(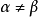 ),顯然,
),顯然, 和
和 均為E的下界,由上面注2可知
均為E的下界,由上面注2可知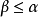 且
且 ,故
,故 . 與假設相矛盾!證畢。
. 與假設相矛盾!證畢。


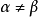


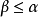


2. 確界存在定理
定理 有上界的非空數集必有上確界,有下界的非空數集必有下確界。
證明:用戴德金分割定理證明。
戴德金定理:對實數集R的任意一個滿足不空、不漏、不亂的劃分A和B,都存在唯一的一個分點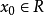 滿足
滿足
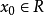

記給定非空集為X。取定B為X的所有上界的集合,A=R\B. 下證A、B為不空、不漏、不亂的劃分。
不空:由於X非空,可取 ,易知x-1不可能為X的上界,故A非空。B非空給定;
,易知x-1不可能為X的上界,故A非空。B非空給定;

不漏:由A=R\B知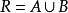 ;
;
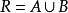
不亂:設 ,則由
,則由 知
知 不是X的上界,即
不是X的上界,即 ,但又由
,但又由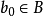 是X的上界知
是X的上界知 . 綜上,
. 綜上, 又
又 ,矛盾。不亂得證。
,矛盾。不亂得證。




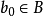



故存在唯一的一個分點 滿足
滿足 下證分點為上確界,即
下證分點為上確界,即 .
.



若不然, 不成立,則
不成立,則 ,但此時就有
,但此時就有 ,由
,由 知
知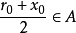 ,與
,與 是劃分A和B的分點相矛盾。故
是劃分A和B的分點相矛盾。故 .
.




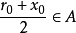


下確界同理。證畢。
3. 單調有界數列必有極限
定理 單調有界數列必有極限。
證明:我們只就單調減少的有界數列予以證明。設 有界,則必有下確界
有界,則必有下確界 . 再設
. 再設 是單調減少的,現在證明
是單調減少的,現在證明 恰好就是
恰好就是 的極限,即
的極限,即 .
.






由下確界的定義有(i) ;(ii)對任意給定的
;(ii)對任意給定的 ,在
,在 中至少有一數
中至少有一數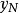 ,有
,有 . 但由於
. 但由於 是單調減少數列,因此當
是單調減少數列,因此當 時,有
時,有 ,從而
,從而 . 也就是說,當
. 也就是說,當 時,有
時,有



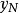






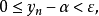

這裡不僅證明了單調有界數列的極限存在,而且也證明了如果它是單調減少的,則極限就是它的下確界。同樣可證單調增加有界數列的極限存在,並且極限就是它的上確界。

