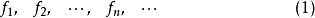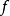一致收斂判別法是判定函式列與函式項級數是否收斂的重要方法,其中比較著名的有柯西準則、魏爾斯特拉斯判別法以及阿貝爾判別法等,它們是數學分析中重要的理論基礎。
基本介紹
- 中文名:一致收斂判別法
- 外文名:uniform convergence test
- 學科:數學
- 領域範圍:數學分析
- 屬性:函式列與函式項級數
函式列及其一致收斂性,定義1,定理1(函式列一致收斂的柯西準則),函式項級數及其一致收斂性,定義2,定理2(一致收斂的柯西準則),函式項級數的一致收斂性判別法,定理3(魏爾斯特拉斯判別法),定理4(阿貝爾判別法),
函式列及其一致收斂性
設
對於函式列,我們不僅要討論它在哪些點上收斂,而更重要的是要研究極限函式所具有的解析性質。比如能否由函式列每項的連續性判斷出極限函式的連續性。又如極限函式的導數和積分,是否分別是函式列每項導數或積分的極限。對這些問題的討論,只要求函式列在數集D上的收斂是不夠的,必須對它在D上的收斂性提出更高的要求才行,這就是以下所要討論的一致收斂性問題。
定義1
設函式列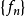 與函式
與函式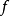 定義在同一數集D上,若對任給的正數
定義在同一數集D上,若對任給的正數 ,總存在某一正整數N,使得當
,總存在某一正整數N,使得當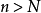 時,對一切
時,對一切 ,都有
,都有
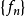
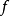

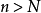


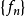





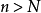
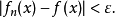


定理1(函式列一致收斂的柯西準則)
函式列 在數集D上一致收斂的充要條件是:對任給正數
在數集D上一致收斂的充要條件是:對任給正數 ,總存在正數N,使得當
,總存在正數N,使得當 時,對一切
時,對一切 ,都有
,都有




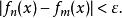
函式項級數及其一致收斂性
設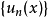 是定義在數集E上的一個函式列,表達式
是定義在數集E上的一個函式列,表達式
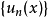

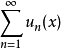
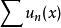

若 ,數項級數
,數項級數

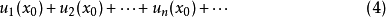
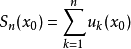
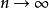
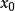
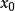
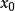

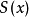
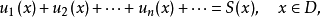

定義2
設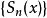 是函式項級數
是函式項級數 的部分和函式列。若
的部分和函式列。若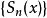 在數集D上一致收斂於
在數集D上一致收斂於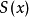 ,則稱
,則稱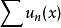 在
在 上一致收斂於
上一致收斂於 。
。
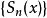

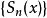
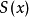
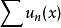


定理2(一致收斂的柯西準則)
函式項級數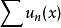 在數集D上一致收斂的充要條件為:對任給的正數
在數集D上一致收斂的充要條件為:對任給的正數 ,總存在某正整數N,使得當
,總存在某正整數N,使得當 時,對一切
時,對一切 和一切正整數
和一切正整數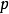 ,都有
,都有
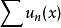



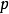
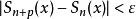
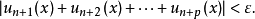
函式項級數的一致收斂性判別法
定理3(魏爾斯特拉斯判別法)
設函式項級數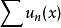 定義在數集D上,
定義在數集D上, 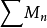 為收斂的正項級數,若對一切
為收斂的正項級數,若對一切 ,有
,有
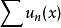
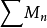


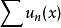
下面討論定義在區間 上形如
上形如

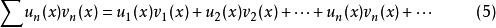
定理4(阿貝爾判別法)
設
(i)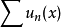 在區間
在區間 上一致收斂;
上一致收斂;
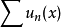

(ii)對於每一個 ,
,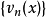 是單調一致有界的;
是單調一致有界的;

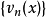
(iii)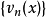 在
在 上一致有界,即對一切
上一致有界,即對一切 和正整數n,存在正數M,使得
和正整數n,存在正數M,使得
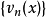


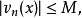
則級數(5)在 上一致收斂。
上一致收斂。