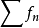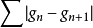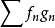戴德金判別法

戴德金判別法是級數收斂的判別法之一。若級數∑a_n的部分和序列有界，b_n→0，∑|b_n-b_n+1|收斂，則級數∑a_nb_n收斂。

基本介紹

• 中文名：戴德金判別法
• 外文名：Dedekind test
• 適用範圍：數理科學

簡介

戴德金判別法是級數收斂的判別法之一。

若級數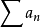的部分和序列有界，b_n→0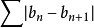，收斂，則級數收斂。

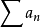
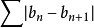
一致收斂性的判別

若函式級數的部分和序列有界，{g_n}一致收斂於0，一致收斂，則函式項級數一致收斂。

收斂級數

（convergent series）

收斂級數是柯西於1821年引進的，它是指部分和序列的極限存在的級數。收斂級數分條件收斂級數和絕對收斂級數兩大類，其性質與有限和（有限項相加）相比有本質的差別，例如交換律和結合律對它不一定成立。

收斂級數的基本性質主要有：級數的每一項同乘一個不為零的常數後，它的收斂性不變；兩個收斂級數逐項相加或逐項相減之後仍為收斂級數；在級數前面加上有限項，不會改變級數的收斂性；原級數收斂，對此級數的項任意加括弧後所得的級數依然收斂；級數收斂的必要條件為級數通項的極限為0。