緊集是指拓撲空間內的一類特殊點集,它們的任何開覆蓋都有有限子覆蓋。從某種意義上,緊集類似於閉集。
基本介紹
- 中文名:緊集
- 外文名:Compact set
- 所屬學科:數學
- 內涵:特殊點集
- 相關概念:有界、閉集、收斂的子序列等
定義
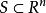
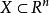
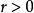
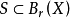
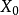
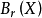
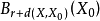
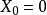
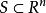
相關概念














相關性質定理
定理1
定理2

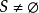




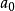


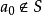


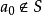
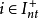
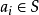
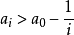


定理3






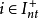










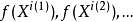


定理4


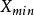
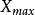





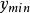
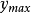
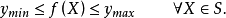
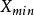
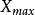

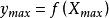
緊集是指拓撲空間內的一類特殊點集,它們的任何開覆蓋都有有限子覆蓋。從某種意義上,緊集類似於閉集。
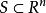
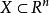
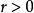
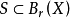
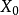
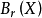
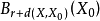
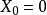
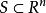















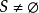




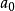


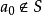


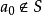
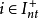
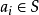
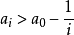








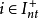










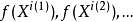




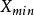
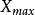





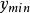
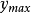
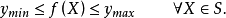
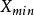
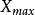

緊集是指拓撲空間內的一類特殊點集,它們的任何開覆蓋都有有限子覆蓋。從某種意義上,緊集類似於閉集。...
列緊集是度量空間中的一類子集,設A是度量空間X中的無窮集,如果A中的任一無窮子集必有一個收斂的點列,就稱A是X中的列緊集;如果X本身是列緊集,就稱X是列...
緊性為點集拓撲中的基本概念,若X的任一開覆蓋有有限子覆蓋,稱拓撲空間X的子集K為緊集,若能從X的任一覆蓋K的開集族中取有限覆蓋。...
預緊(precompact)是數學中的一個基本概念,主要出現在分析學中。一個集合稱為預緊,則該集合的閉包為緊集。...
緊緻集是拓撲空間的一類重要子集,亦稱緊緻集。稱A為緊集,若A的任意開覆蓋包含A的有限開覆蓋。有限維賦范線性空間中的有界閉集是緊集。...
緊連續映射(compact continuous mapping)是像集為相對緊集的連續映射,簡稱緊映射。...... 緊連續映射(compact continuous mapping)是像集為相對緊集的連續映射,簡稱...
完全有界集是指距離空間中的一類子集。度量空間中的列緊集一定是完全有界的,而在完備度量空間中,完全有界性與列緊性等價。...
完全映射(perfect mapping)亦稱完備映射,一類重要的映射。設X,Y為拓撲空間,映射f:X→Y。若對於任意y∈Y,f(y)是X的緊集,則稱f為緊映射。若f是緊的、閉的...
對R的緊集F(無限集),關於對數核K(x)=-log|x|,當m→∞時,單調增加,把exp[-Bm(F)]的極限d(F)稱為F的超限直徑,那么d(F)=Cl(F),它還等於F的切...
設X、Y均為距離空間,T為X→Y的線性運算元,如果T將X中的任一有界集映成Y中的列緊集,則T稱為緊運算元,連續的緊運算元稱作全連續運算元。如果X、Y均為賦范線性空間...
設X是局部緊的豪斯多夫空間,𝒰是X上的超調和簇,U是開集。若對f∈𝒰(U),存在緊集K使得在U\K上f≥0,並且∀ξ∈∂U,當x→ξ時lim inf f(x)≥...
