MP集

設X是局部緊的豪斯多夫空間，𝒰是X上的超調和簇，U是開集。若對f∈𝒰(U)，存在緊集K使得在U\K上f≥0，並且∀ξ∈∂U，當x→ξ時lim inf f(x)≥0，則在U上f≥0，那么稱U為MP集。

基本介紹

• 中文名：MP集
• 外文名：MP-set
• 適用範圍：數理科學

簡介

MP集是使某種形式的極小值原理成立的開集。

設X是局部緊的豪斯多夫空間，𝒰是X上的超調和簇，U是開集。若對f∈𝒰(U)，存在緊集K使得在U\K上f≥0，並且∀ξ∈∂U，當x→ξ時lim inf f(x)≥0，則在U上f≥0，那么稱U為MP集。

極小值原理

控制向量u(t)受限制的情況下，使哈密頓函式取極小，求解最優控制問題的原理和方法，又稱極大值原理。

極小值原理是在20世紀50年代由蘇聯學者龐特里雅金(Л.С.Понтрягин)提出的，它的結果與古典變分法極為近似。但它克服了古典變分法的局限性，適用範圍擴大了。原先提出時，稱為“極大值原理”，兩者是一致的，因為一個函式的極小與其反號函式的極大是相同的。

緊集

緊集是指拓撲空間內的一類特殊點集，它們的任何開覆蓋都有有限子覆蓋。從某種意義上，緊集類似於閉集。

如果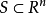是有界的閉集，那么S是緊集。