控制向量u(t)受限制的情況下,使哈密頓函式取極小,求解最優控制問題的原理和方法,又稱極大值原理。
基本介紹
- 中文名:極小值原理
- 外文名:minimum principle
- 學科:電力科學
- 拼音:jixiaozhi yuanli
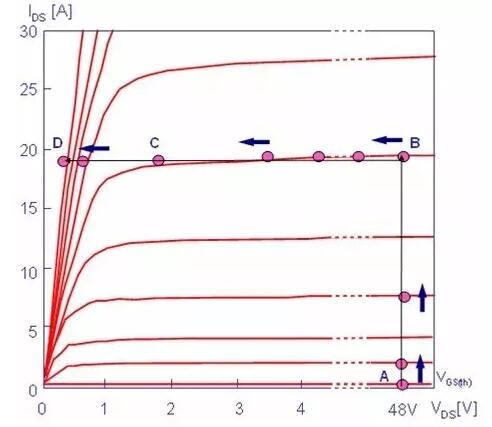
控制向量u(t)受限制的情況下,使哈密頓函式取極小,求解最優控制問題的原理和方法,又稱極大值原理。
控制向量u(t)受限制的情況下,使哈密頓函式取極小,求解最優控制問題的原理和方法,又稱極大值原理。...
極大值原理是對分析力學中古典變分法的推廣,能用於處理由於外力源的限制而使系統的輸入(即控制)作用有約束的問題。極大值原理是20世紀50年代中期蘇聯學者Л.С....
最小勢能原理就是說當一個體系的勢能最小時,系統會處於穩定平衡狀態。舉個例子...但其實只要你不動你也是平衡的,因為駐值也可以是極大值(此時稱為隨遇平衡)。...
弱極大值原理(weakmaxtmumprinciple)階橢圓方程的一個重要特性.在一定條件下,在區域 內滿足微分方程(或微分不等式)的解的最大值必在 區域邊界上達到.設偏微分...
第一極大值原理(first maximum principle)是描述位勢局部極大值蘊涵整體極大值的一個原理。...
廣義極大值原理是第一極大值原理的推廣。α核都滿足廣義極大值原理。...... 廣義極大值原理是第一極大值原理的推廣。α核都滿足廣義極大值原理。...
(2)極大值原理:在用變分法求解最優控制問題時,是假定控制向量u(O)不受任何限制,即容許控制集合可以看成是整個P維控制空間開集,控制變分u是任意的,同時還...
但由最值原理,如果最值存在,此方程組求得的駐點即為所求的最值點,就可以很到參數的極大似然估計。極大似然估計法一般屬於這種情況,所以可以直接按上述步驟求極...
如果目標函式有明顯的表達式,一般可用微分法、變分法、極大值原理或動態規劃等分析方法求解(間接選優);如果目標函式的表達式過於複雜或根本沒有明顯的表達式,則可用...
解決最優控制問題的主要方法有古典變分法、極大值原理和動態規劃。而線性最優控制問題,它的解可以由轉移函式表出,特別是在定常情況下,轉移函式有具體表達式,從而...
微分對策的最優策略所應滿足的必要條件,可象最優控制理論中的極大值原理那樣導出。微分對策實質上是一種雙(多)方的最優控制問題,而通常的最優控制問題可看成是...
調和函式極大值定理 調和函式滿足以下的極大值定理:如果K是U的一個緊子集,那么f在K上誘導的函式只能在邊界上達到其最大值和最小值。如果U是連通的,那么這個...
動態規劃原理可用來將變分法問題歸結為多階段決策過程,用動態規劃的貝爾曼方程求解。在最優控制理論中動態規劃方法比極大值原理更為適用 [1] ,但動態規劃還缺少...
