基本介紹
- 中文名:滿射
- 外文名:surjection
- 定義:對任意b,存在a滿足f(a) = b
- 所屬學科:初等數學
- 套用學科:數學
- 相關術語:滿射函式
定義
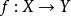


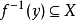
例子和反例
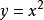


性質



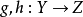
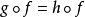




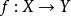


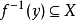
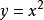





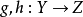
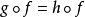



一個函式稱為滿射:如果每個可能的像至少有一個變數映射其上(即像集合B中的每個元素在A中都有一個或一個以上的原像),或者說陪域任何元素都有至少有一個變數與...
滿射線性運算元亦稱為映到上的線性運算元,是值域等於全空間的線性運算元。...... (T)到E上的一對一滿射的線性運算元,而且λI-T的逆運算元(λI-T)-1是E到E的有界線...
既是單射又是滿射的映射稱為雙射,亦稱“一一映射”。雙射(Bijection)的原理是一組關係,在判別某一種想法在套用能否雙向的找到某一唯一對應的事物,理論上通常要...
注意:(1)對於A中不同的元素,在B中不一定有不同的象;(2)B中每個元素都有原象(即滿射),且集合A中不同的元素在集合B中都有不同的象(即單射),則稱映射f...
是滿射若且唯若 是單射。康托爾定理髮展簡史 編輯 康托爾在1891年發表的論文"Über eine elementare Frage der Mannigfaltigkeitslehre"中本質上給出了這個證...
數學上,單射、滿射和雙射指根據其定義域和陪域的關聯方式所區分的三類函式。單射:指將不同的變數映射到不同的值的函式。滿射:指陪域等於值域的函式, 即:對...
既是單射又是滿射的線性運算元稱為雙射線性運算元(bijective linear operator)。...... 滿射線性運算元是值域等於全空間的線性運算元,亦稱為映到上的線性運算元。...
在範疇論中,正規態射是一類可以自然地分解成單射與滿射的態射。使所有態射皆為正規態射的範疇稱為正規範疇。...
在泛函分析中,開映射是一類特殊的映射。如果巴拿赫空間之間的連續函式是滿射的,那么它就是一個開映射(open mapping)。如果X和Y是巴拿赫空間,A : X → Y是一個...
自然映射是一種重要的映射,亦稱正規映射、典型映射。自然映射是滿射;反之,若f為滿射,則f可分解為一個自然映射與一個雙射的積。...
滿態射是集合範疇中滿射概念的推廣。它是單態射的對偶概念。範疇C中的態射f:A→B,若有右可消性質,即由態射合成uf=vf可斷定u=v,則稱f為C中的滿態射。...
在泛函分析中,開映射定理是一個基本的結果,它說明如果巴拿赫空間之間的連續線性運算元是滿射的,那么它就是一個開映射。更加精確地:該定理的證明用到了貝爾綱定理,X...
是從集合A到集合B的一個滿射。(3)如果函式 既是從集合A到集合B的一個單射.又是從集合A到集合B的一個滿射,則稱它是從集合A到集合B的一個雙射。 [2] 函...
精確地(Rudin 1973, 定理2.11):如果X和Y是巴拿赫空間,A : X→ Y是一個滿射的連續線性運算元,那么A就是一個開映射(也就是說,如果U是X內的開集,那么A(U)...
