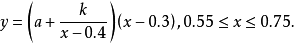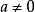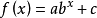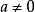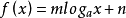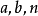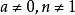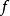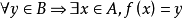函式關係

確定性現象之間的關係常常表現為函式關係，即一種現象的數量確定以後，另一種現象的數量也隨之完全確定，表現為一種嚴格的函式關係。當一個或幾個變數取一定的值時，另一個變數有確定值與之對應，則稱這種關係為確定性的函式關係，記為y=f(x)，其中x稱為自變數，y稱為因變數。

例如，某種商品的銷售額y與銷售量x之間的關係可表示為y=px(p為單價)；圓的面積S與半徑R之間的關係可表示為S=πR²；企業的原材料消耗額Y與產量X₁、單位產量消耗X₂、原材料價格X₃之間的關係可表示為Y=X₁X₂X₃；一隻股票的成交額與該股票的成交量之間的關係，保持成交價格P不變的情況下，當股票的成交量X確定後，其成交額Y也隨之確定，三者之間的關係是：Y=PX。

函式關係常用的三種表示方法是列表法，解析法，圖象法。

基本介紹

• 中文名：函式關係
• 外文名：functional relationship
• 所屬學科：數學
• 特點：一個變數有唯一確定值與之相對應
• 相關概念：定義域、值域、相關關係等

定義

設A和B是兩個給定的集合， 是從集合A到集合B的一個二元關係。如果這個二元關係還滿足下面的性質：對每個元素 ，存在唯一的元素 ，使得二元序偶 ，就稱這個二元關係是從集合A到集合B的一個函式或者映射。記作

或者

也可改寫為 ，其中y稱為x的象，而x則稱為y的原象。稱集合A是函式的定義域，集合A中所有元素在函式 的作用下得到的所有象的集合稱為函式 的象或函式 的值域。

為了進一步區分不同特性的函式，給出細分的定義。

設 是從集合A到集合B的一個函式。

(1)如果 ，則稱函式 是從集合A到集合B的一個單射。

(2)如果 ，則稱函式 是從集合A到集合B的一個滿射。

(3)如果函式 既是從集合A到集合B的一個單射．又是從集合A到集合B的一個滿射，則稱它是從集合A到集合B的一個雙射。

注意點

關於函式定義的幾點說明：

(1)如果 是從集合A到集合B的一個函式，那么集合A中每個元素必須都有象，且象必須唯一。

(2)如果 是從集合A到集合B的一個函式．那么集合B中每個元素不一定都有原象，且當有原象時，原象也不一定唯一。

(3)根據函式的定義可知，兩個函式是否相等。需要看：二者的定義域是否相同；對於定義域內的每一個元素．它在這兩個函式作用下的象是否恆相同。

函式關係的建立

方法步驟

對於實際問題，明確其中各種量及量之間的關係，建立正確的函式關係十分重要。在建立函式關係時，首先要確定問題中的自變數與因變數，再根據它們之間的關係列出等式，得出函式關係式，然後確定函式定義域，確定定義域時，不僅要考慮到函式關係的解析式，還要考慮到變數在實際問題中的含義。

建立函式關係的基本步驟：

①明確問題中的因變數與自變數，並以適當記號表示；

②尋找等量關係，建立函式關係；

③確定函式的定義域。

舉例說明

下面舉例說明如何建立函式關係。

例1 某商場銷售某種商品8000件，每件原價70元，當銷售量在5000件以內(包含5000件)時，按照原價出售，超過5000件部分，打八折銷售。試建立總銷售收入與銷售量之問的函式關係。

解：設銷售量為x件，總銷售收入為R元，總銷售收人與銷售量之間的函式關係為

例2 某工廠生產某種型號的車床，年產量為a台，分若干批次進行生產，每批次的生產準備費為b元，設產品均勻投入市場，且上一批用完後立即生產下一批，即平均庫存量為批量的一半，設每年每台庫存費為c元，顯然，生產批量大則庫存費高；生產批量少則批數增多，因而生產準備費高，為了選擇最優批量，試求出一年中庫存費與生產準備費的和與批量之問的關係。

解：設批量為x，庫存費與生產準備費的和為P(x)，因年產量為a，所以每年生產的批數為 (設其為整數)，則生產準備費為 ，因庫存量為a，故庫存費為 ，因此可得

定義域為(0，a]，因本題中的x為車床的台數，批數 為整數，所以x只應取(0，a]中的a的正整數因子。

例3 某牧場要建造占地100m²的矩形圍牆，現有一排長20m的舊牆可供利用，為了節約投資，矩形圍牆的一邊直接用舊牆修，另外三邊儘量用拆去的舊牆改建，不足部分用購置的新磚新建，已知整修1m舊牆需24元，拆去1m舊牆改建成1m新牆需100元，建造1m新牆需200元，設舊牆所保留的部分用x表示，整個投資用y表示，將y表示為x的函式。

解：整個投資的費用包括整修舊牆的費用、拆舊改新的費用以及建造新牆的費用，所以所求函式關係為

例4 某地區上年度電價為0.8元/(kW·h)，年用電量為a kW·h，本年度將電價降到0.55元/(kW·h)至0.75元/(kW·h)之間，而用戶期望電價為0.4元/(kW·h)，經測算，下調電價後新增的用電量與實際電價和用戶期望電價的差成反比(比例係數為k)，該地區的電力成本為0.3元/(kW·h)，寫出本年度電價下調後，電力部門的收益y與實際電價x的函式關係式。

解：收益=實際用電量×(實際電價-成本價)。

所以所求函式關係式為

幾類常見的函式關係模型

一次函式模型

(為常數，).

反比例函式模型

(為常數，).

二次函式模型

(為常數，).

指數型函式模型

(為常數，，).

對數型函式模型

(為常數，，).

冪型函式模型

(為常數，).

函式關係與相關關係的區分

相關關係的定義

當變數X取某個值時，變數Y的取值可能有若干個，這些數值表現為一定的波動性，但總是圍繞著它們的平均數，並遵循一定的規律變動。變數之間存在的這種不確定的數量關係稱為相關關係。特點：Y與X的值不一一對應；Y與X的關係不能用函式式嚴格表達，但有規律可循。

例如：父親身高Y與子女身高X之間的關係；收入水平Y與受教育程度X之間的關係；糧食畝產量Y與施肥量X₁、降雨量X₂、溫度X₃之間的關係；商品的消費量Y與居民收入X之間的關係；商品銷售額Y與廣告費支出X之間的關係。

二者的的區分

區分相關關係與函式關係的依據全憑因變數取值的確定性：若因變數的取值是確定的、唯一的，則兩個變數之間的關係稱為函式關係；若因變數的取值是不確定的，則兩個變數之間的關係稱為相關關係。

例5 試判定下列變數之間屬於函式關係，還是相關關係。

(1)圓面積與圓半徑 (2)價格確定下商品的銷售額與銷售量

(3)人們的身高與體重 (4)商品廣告費支出與銷售額

(5)家庭月收入與月支出 (6)施肥量與畝產量

(7)文化程度與年收入 (8)圖書印數與圖書價格

(9)商品銷售額與商品流通費用率 (10)可變銷售價格與商品銷售額

解：按照函式關係和相關關係的定義與區別，本例中，第(1)、第(2)為函式關係，其餘均為相關關係。

注意：變數之間的函式關係和相關關係在一定條件下是可以相互轉化的。本來具有函式關係的變數，在存在觀測誤差時，其函式關係往往以相關的形式表現出來。而具有相關關係的變數之間的聯繫，如果對其有深刻的規律性認識，並且能夠把影響因變數變化的因素全部納入方程，這時相關關係也可能轉化為函式關係。另外，相關關係也具有某種變動規律性，所以，相關關係經常可以用一定的函式形式去近似地描述。客觀現象的函式關係可以用數學分析的方法研究，而研究客觀現象的相關關係，則必須藉助於統計學中的相關與回歸分析方法。