基本介紹
函式符號的歷史




函式概念的發展
早期--幾何觀念
十八世紀--代數觀念
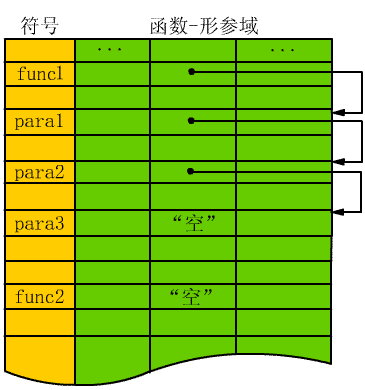 函式符號
函式符號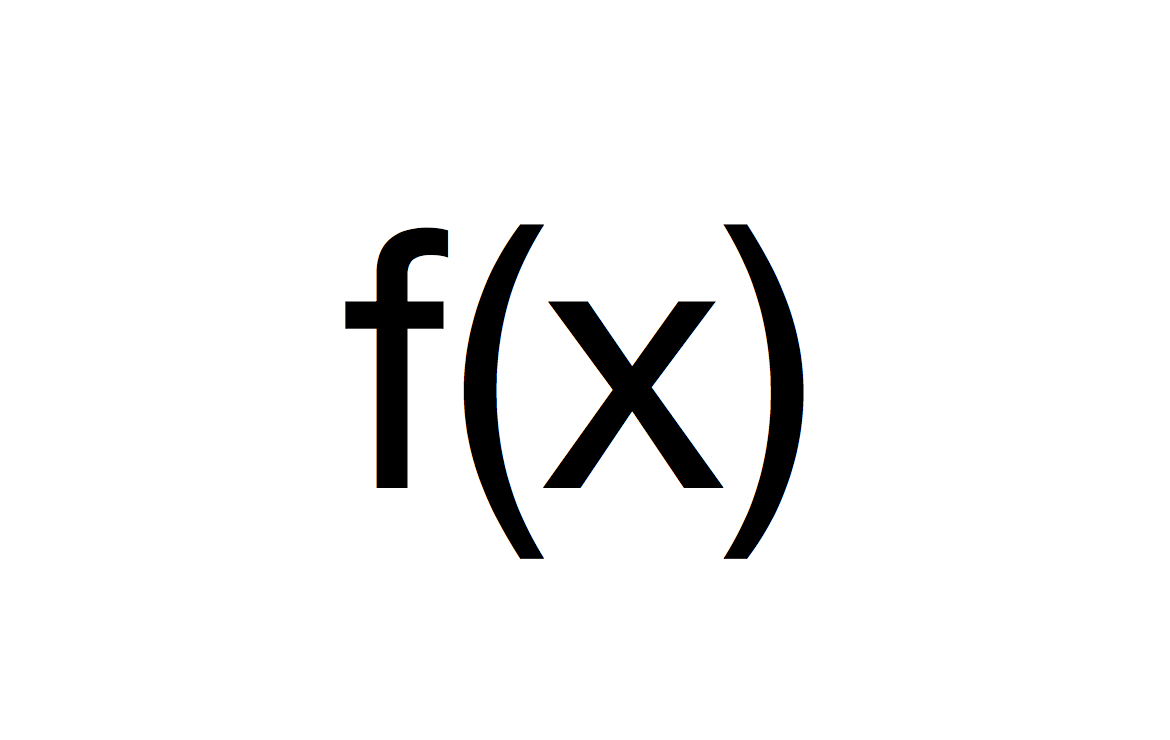




 函式符號
函式符號約翰.伯努利於1694年首次提出函式(function)概念,並以字母 n 表示變數 z 的一個函式;至 1697年,他又以大寫字母 X 及相應之希臘字母 ξ表示變數 x 的函式。...
數學上的Sgn 函式返回一個整型變數,指出參數的正負號。語法Sgn(number), number 參數是任何有效的數值表達式。返回值如果 number 大於0,則Sgn 返回1;等於0,返回0...
sign又叫sgn,意思是符號。符號函式(一般用sign(x)表示)是很有用的一類函式,能夠幫助我們在幾何畫板中實現一些直接實現有困難的構造。 符號函式 能夠把函式的符號...
毛羅利科早於1558年已採用三角函式符號(Signs for trigonometric functions), 但當時並無函式概念,於是只稱作三角線( trigonometric lines)。他以sinus 1m arcus 表示...
數學符號的發明及使用比數字要晚,但其數量卻超過了數字。現代數學常用的數學符號已超過了200個,其中,每一個符號都有一段有趣的經歷。...
在數學領域,函式是一種關係,這種關係使一個集合里的每一個元素對應到另一個(可能相同的)集合里的唯一元素。...
關係符號(relational symbols)是表示數與數、式與式之間的某種關係的特定記號,這種關係符號有大於號、小於號、等於號、約等於號等。...
● 在函式 中表示向左向右平移大小。● 立體坐標中,一直線與 z-軸之間的夾角。● 體積分數,符號為 φ,當指物質 B 體積分數時,符號 φB或φ(B),定義為:...
瓦尼爾函式(Wannier function,或沃尼埃函式),是固體物理學中的一個正交函式的完備集,由格里高利·瓦尼爾提出。瓦尼爾函式在晶系中對應著局域化分子軌道。晶體中不同...
大O符號(Big O notation)是用於描述函式漸進行為的數學符號。更確切地說,它是用另一個(通常更簡單的)函式來描述一個函式數量級的漸近上界。在數學中,它一般用來...
正割指的是直角三角形,斜邊與某個銳角的鄰邊的比,叫做該銳角的正割,用 sec(角)表示。正割是餘弦函式的倒數。...
邏輯符號,指的是在邏輯中,經常使用的一組來表達邏輯結構的符號。不同的符號有相同的意義。如:A ⇒ B 意味著如果 A 為真,則 B 也為真;如果 A 為假,則...
階躍函式,數學上的符號函式或者計算機語言中的返回函式。Sgn 函式 返回一個 Variant (Integer),指出參數的正負號。 語法 Sgn(number) 必要的 number 參數是任何...
L符號是個類似大O符號的漸近符號,多用於表示特定算法的計算複雜性。...... 當 介於0與1之間時,L符號為lnn的次指數(與超越多項數)函式。 [1] ...
符號函式(一般用sign(x)表示)是很有用的一類函式,能夠幫助我們在幾何畫板中實現一些直接實現有困難的構造。 符號函式 能夠把函式的符號析離出來 。在數學和計算機...
笛卡爾符號法則由笛卡爾首先提出,用於分析高次多項式正根與負根的個數。...... 笛卡兒符號法則(Descartes' rule of signs)是高次多項式函式(Higher-Degree Polynomial...
微分符號是1675年萊布尼茲分別引入「dx」及「dy」以表示x和y的微分(differentials),.始見於他在1684年出版的書中,這符號一直沿用至今.微分符號d取英文differential,...
符號計算又稱計算機代數,通俗地說就是用計算機推導數學公式,如對表達式進行因式分解、化簡、微分、積分、解代數方程、求解常微分方程等。...
函式(function)表示每個輸入值對應唯一輸出值的一種對應關係。函式f中對應輸入值的輸出值x的標準符號為f(x)。包含某個函式所有的輸入值的集合被稱作這個函式的定義...
