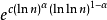L符號

L符號是個類似大O符號的漸近符號，多用於表示特定算法的計算複雜性。

基本介紹

• 中文名：L符號
• 外文名：L-notation
• 分類：計算機複雜性

定義

L符號的定義如下：

其中，c為一正實數，且 為一實數 。

L符號主要用於計算數論，表示困難數論問題之算法的複雜性，如整數分解的篩法及離散對數的解法。L符號可簡化對這些算法的分析，以 表示主要項， 則用以表示其他較小的項。

當 為0時，

是個lnn的多項式函式；而當為1時，

則會是lnn的指數函式（即n的多項式函式）。

當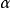介於0與1之間時，L符號為lnn的次指數（與超越多項數）函式。

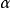
例子

許多通用的整數分解算法都具有次指數複雜度，其中目前已知最快的為普通數域篩選法，其時間複雜度估算為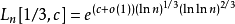

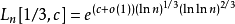
其中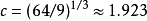，。在普通數域篩法出現前，最快的整數分析算法為二元篩法，其時間複雜度估算為

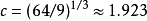
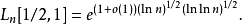
對橢圓曲線離散對數問題而言，目前已知最快的通用算法為大步小步法，其時間複雜估算為群階的開平方。以L符號表示為

目前已知最快測試一個數是否為質數的算法為AKS質數測試，其時間複雜度為多項式時間，以L符號表示為

其中，c已被證明至多為6

歷史

最早出現L符號的文獻為卡爾·帕梅朗斯所著的論文《一些整數分解算法的分析與比較》（Analysis and comparison of some integer factoring algorithms）。在此論文中，L符號的參數只有，其中的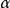則因其所分析的算法而設為。

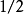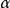
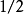
具有兩個參數的L符號則由阿爾揚·倫斯特拉及亨德里克·倫斯特拉在其論文《數論中的算法》（Algorithms in Number Theory）中首次引入，用以分析唐·科普斯密思的離散對數算法，為現在數學文獻中最常使用的形式。