基本介紹
定義
算法複雜度
時間複雜度
計算方法
for(i=1; i<=n; ++i){ for(j=1; j<=n; ++j) { c[i][j] = 0;//該步驟屬於基本操作執行次數:n的平方次 for(k=1; k<=n; ++k) c[i][j] += a[i][k] * b[k][j];//該步驟屬於基本操作執行次數:n的三次方次 }}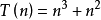

分類

for(i=1; i<=n; ++i){ for(j=1; j<=n; ++j) { c[i][j] = 0;//該步驟屬於基本操作執行次數:n的平方次 for(k=1; k<=n; ++k) c[i][j] += a[i][k] * b[k][j];//該步驟屬於基本操作執行次數:n的三次方次 }}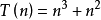


時間複雜度是同一問題可用不同算法解決,而一個算法的質量優劣將影響到算法乃至程式的效率。算法分析的目的在於選擇合適算法和改進算法。計算機科學中,算法的時間複雜...
算法複雜度是指算法在編寫成可執行程式後,運行時所需要的資源,資源包括時間資源和記憶體資源。套用於數學和計算機導論。...
在計算機科學中,時間複雜性,又稱時間複雜度,算法的時間複雜度是一個函式,它定性描述該算法的運行時間。這是一個代表算法輸入值的字元串的長度的函式。時間複雜度...
複雜度(Complexity, CPX),指的是在給定樣本中不同DNA 序列的總長度,是一件事物的複雜性可以用描寫這事物所需的計算機語言的長度來衡量。...
漸進時間複雜度是指對於一個算法來說,我們常常需要計算其複雜度來決定我們是否選擇使用該算法。...
非定常多項式(英語:non-deterministic polynomial,縮寫:NP)時間複雜性類,或稱非確定性多項式時間複雜性類,包含了可以在多項式時間內,對一個判定性算法問題的實例,一...
P的擴大集合是NP,此複雜度類別是一個可在多項式時間以非確定型圖靈機決定答案的問題的集合。因此我們可知道P是NP的子集,且雖然未證明,但大部分專家相信P是NP的...
算法複雜性分析時間複雜度 通常,對於一個算法的複雜性分析主要是對算法效率的分析,包括衡量其運行速度的時間效率及衡量其運行時所需要占用空間大小的空間效率。...
算法複雜性時間複雜度 編輯 一般情況下,對於一個算法的複雜性分析主要是對算法效率的分析,包括衡量其運行速度的時間效率及衡量其運行時所需要占用空間大小的空間效率...
所謂"計算複雜性",通俗說來,就是用計算機求解問題的難易程度。其度量標準:一是計算所需的步數或指令條數(這叫時間複雜度),二是計算所需的存儲單元數量(這叫...
計算複雜性的初衷是理解不同算法問題的難度,特別的是一些重要算法問題的困難性。為了確切的描述一個問題的困難性,計算複雜性的第一步抽象是認為多項式時間是有效的,...
時間複雜度和大O表示法當問題規模即要處理的數據增長時, 基本操作要重複執行的次數必定也會增長, 那么我們關心地是這個執行次數以什麼樣的數量級增長。所謂數量級...
算法的時間複雜度是指執行算法所需要的計算工作量。一般來說,計算機算法是問題規模n 的函式f(n),算法的時間複雜度也因此記做。T(n)=Ο(f(n))...
參數算法(parameterized algorithm)是基於參數複雜度理論(parameterized complexity)設計的一類算法,其運行時間複雜度可以寫成f(k)*n^c的形式,其中k是我們的參數。參數...
當要計算某個算法的時間複雜度F(n)時,可以找一個更簡單的、階數相同的簡單算法g(n)等同計算,這裡的g(n)是指替代函式,它具有和原算法一樣更高階複雜度。 ...
最差情形下,BFS必須尋找所有到可能節點的所有路徑,因此其時間複雜度為O(|V| + |E|),其中 |V| 是節點的數目,而 |E| 是圖中邊的數目。...
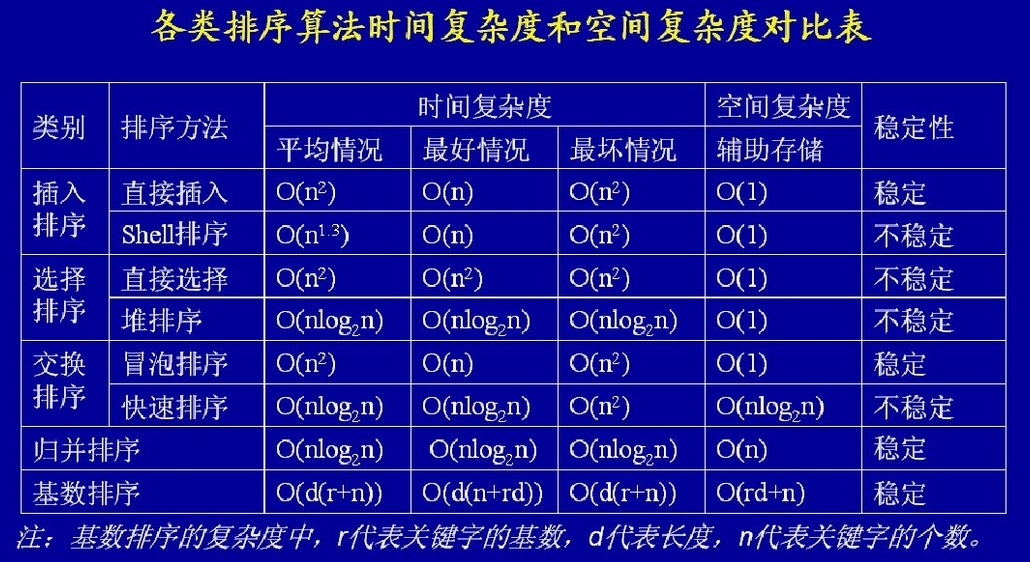
(1)時間複雜度:即從序列的初始狀態到經過排序算法的變換移位等操作變到最終排序好的結果狀態的過程所花費的時間度量。(2)空間複雜度:就是從序列的初始狀態經過...
時間效率 [1] :設待排序列為n個記錄,d個關鍵碼,關鍵碼的取值範圍為radix,則進行鏈式基數排序的時間複雜度為O(d(n+radix)),其中,一趟分配時間複雜度為O(n)...
