算法複雜性的度量主要是針對運行該算法所需要的計算機資源的多少。當算法所需要的資源越多,該算法的複雜性越高;反之,當算法所需要的資源越少,算法的複雜性越低。
對於任意給定的一個問題,設計出複雜性儘可能低的算法是在設計算法時追求的重要目標之一;而當給定的問題存在多種算法時,選擇其中複雜性最低的算法是選用算法時遵循的重要準則。因此,算法的複雜性分析對算法的設計或選用具有重要的指導意義和實用價值。
基本介紹
- 中文名:算法複雜性
- 意義:估算某個算法所消耗的資源
- 種類:時間複雜度、空間複雜度
時間複雜度
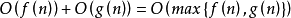
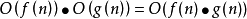
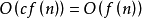

算法複雜性的度量主要是針對運行該算法所需要的計算機資源的多少。當算法所需要的資源越多,該算法的複雜性越高;反之,當算法所需要的資源越少,算法的複雜性越低。
對於任意給定的一個問題,設計出複雜性儘可能低的算法是在設計算法時追求的重要目標之一;而當給定的問題存在多種算法時,選擇其中複雜性最低的算法是選用算法時遵循的重要準則。因此,算法的複雜性分析對算法的設計或選用具有重要的指導意義和實用價值。
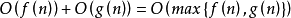
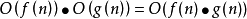
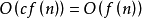
算法複雜性的度量主要是針對運行該算法所需要的計算機資源的多少。當算法所需要的資源越多,該算法的複雜性越高;反之,當算法所需要的資源越少,算法的複雜性越低。...
算法複雜度是指算法在編寫成可執行程式後,運行時所需要的資源,資源包括時間資源和記憶體資源。套用於數學和計算機導論。...
算法複雜性分析(Algorithm complexity analysis)主要是針對運行該算法所需要的計算機資源的多少。當算法所需要的資源越多,該算法的複雜性越高;反之,當算法所需要的...
算法效率的度量,是評價算法優劣的重要依據。一個算法的複雜性的高低體現在運行該算法所需要的計算機資源的多少上面,所需的資源越多,我們就說該算法的複雜性越高;...
在計算機科學中,時間複雜性,又稱時間複雜度,算法的時間複雜度是一個函式,它定性描述該算法的運行時間。這是一個代表算法輸入值的字元串的長度的函式。時間複雜度...
複雜性理論(complexity theory)是理論計算機科學和數學的一個分支,它致力於將可計算問題根據它們本身的複雜性分類,以及將這些類別聯繫起來。一個可計算問題被認為是一...
計算複雜性理論(Computational complexity theory)是理論計算機科學和數學的一個分支,它致力於將可計算問題根據它們本身的複雜性分類,以及將這些類別聯繫起來。一個可...
計算複雜性理論是理論計算機科學的分支學科,使用數學方法對計算中所需的各種資源的耗費作定量的分析,並研究各類問題之間在計算複雜程度上的相互關係和基本性質,是算法...
《可計算性和計算複雜性》是國防工業出版社2006年出版的圖書,作者是朱一清。...... 圖靈機、λ演算、馬爾可夫算法、計算複雜度的分類、NP完全理論、非一致複雜性等...
計算複雜性測度(computational complexitymeasure)簡稱複雜性測度,是對計算複雜性概念的一種定量刻畫。...
《計算複雜性理論基礎》主要講述了,計算複雜性理論是用數學方法研究計算機解決各種算法問題難易程度的理論。《計算複雜性理論基礎》對這一理論的基礎知識做了全面介紹...
複雜度(Complexity, CPX),指的是在給定樣本中不同DNA 序列的總長度,是一件事物的複雜性可以用描寫這事物所需的計算機語言的長度來衡量。...
本書是一本全面闡述計算機複雜性理論及其近年來進展的教科書,主要包含算法圖靈機、可計算性等有關計算複雜理論的基本概念;布爾邏輯、一階邏輯、邏輯中的不可判定性...
時間複雜度是同一問題可用不同算法解決,而一個算法的質量優劣將影響到算法乃至程式的效率。算法分析的目的在於選擇合適算法和改進算法。計算機科學中,算法的時間複雜...
量子複雜性理論(Quantum complexity theory)是理論計算機科學中計算複雜性理論的一部分。...
計算複雜性理論是理論計算機科學的分支學科之一,是指使用數學方法對計算中所需的各種資源的耗費作定量的分析,並研究各類問題之間在計算複雜程度上的相互關係和基本...
複雜性度量(complexity measure)計算複雜性的衡量標準(參見“算法分析”、“計算複雜性理論”、“計算複雜性”等)。這種衡量標準不能表示為絕對的數量大小,而應表示...
《計算複雜性導論》是2002年高等教育出版社出版的圖書,作者是堵丁柱、葛可一、王傑。本書對計算機科學中這一重要理論做了全面的介紹。其內容包含基本理論,如計算...
算法的空間複雜度是指算法需要消耗的記憶體空間。其計算和表示方法與時間複雜度類似,一般都用複雜度的漸近性來表示。同時間複雜度相比,空間複雜度的分析要簡單得多。...
算法的空間複雜度是指算法需要消耗的空間資源。其計算和表示方法與時間複雜度類似,一般都用複雜度的漸近性來表示。同時間複雜度相比,空間複雜度的分析要簡單得多。...
機率算法也叫隨機化算法。機率算法允許算法在執行過程中隨機地選擇下一個計算步驟。在很多情況下,算法在執行過程中面臨選擇時,隨機性選擇比最優選擇省時,因此機率...
“智慧型算法”是指在工程實踐中,經常會接觸到一些比較“新穎”的算法或理論,比如模擬退火,遺傳算法,禁忌搜尋,神經網路等。這些算法或理論都有一些共同的特性(比如...
複雜系統是具有中等數目基於局部信息做出行動的智慧型性、自適應性主體的系統。複雜系統是相對牛頓時代以來構成科學事業焦點的簡單系統相比而言的,具有根本性的不同。簡單...
許多時候要精確的計算T(n)是困難的,引入漸進時間複雜度在數量上估計一個算法的執行時間,也能夠達到分析算法的目的。分析計算法空間複雜度 編輯 ...
搜尋算法是利用計算機的高性能來有目的的窮舉一個問題解空間的部分或所有的可能情況,從而求出問題的解的一種方法。現階段一般有枚舉算法、深度優先搜尋、廣度優先...
衡量隨機算法的時間複雜性,是對確定實例I的期望運行時間,即反覆地運行實例I,所取的平均運行時間。在隨機算法里,所討論的是最壞情況下的期望時間,和平均情況下的...
確定型時間複雜性測度(deterministic timecomplexity measure)一種複雜性測度.它是以計算步數為度量的複雜性測度...
