隨機算法是一個概念圖靈機,也就是在算法中引入隨機因素,即通過隨機數選擇算法的下一步操作。
基本介紹
- 中文名:隨即算法
- 外文名:randomized algorithm
基本概念
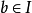
背景及歷史
重要方法
重要人物和工作
類型分類
時間複雜性
隨即算法的設計方法
隨機算法舉例
Quick Sort
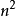
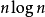
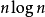
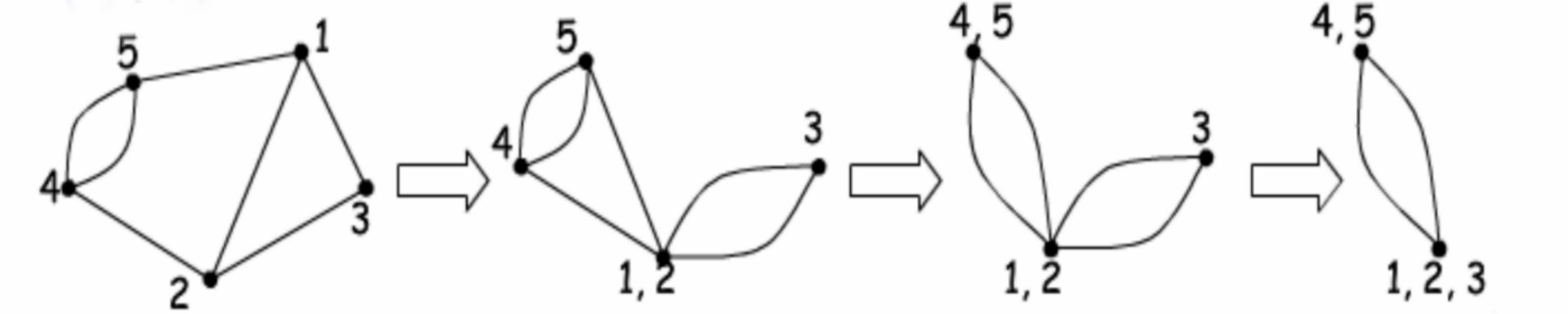
Min Cut
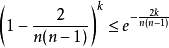

隨機算法是一個概念圖靈機,也就是在算法中引入隨機因素,即通過隨機數選擇算法的下一步操作。
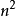
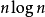
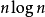
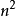

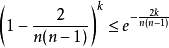
隨機算法是一個概念圖靈機,也就是在算法中引入隨機因素,即通過隨機數選擇算法的下一步操作。...
隨機化算法(randomized algorithm),是這樣一種算法,在算法中使用了隨機函式,且隨機函式的返回值直接或者間接的影響了算法的執行流程或執行結果。就是將算法的某一步...
機率算法也叫隨機化算法。機率算法允許算法在執行過程中隨機地選擇下一個計算步驟。在很多情況下,算法在執行過程中面臨選擇時,隨機性選擇比最優選擇省時,因此機率...
加權隨機算法是深度學習中的常見算法,一般套用在以下場景:有一個集合S,裡面比如有A,B,C,D這四項。這時我們想隨機從中抽取一項,但是抽取的機率不同,比如我們希望...
隨機化算法是這樣一種算法,在算法中使用了隨機函式,且隨機函式的返回值直接或者間接的影響了算法的執行流程或執行結果。隨機化算法基於隨機方法,依賴於機率大小。...
隨機建模技術是指利用一個地質體某一屬性已知的結構統計‘特徵,通過一些隨機算法來模擬未知區這一屬性的分布,使其與已知的統計特徵相同,從而達到模擬儲層非均質性,...
算法(Algorithm)是指解題方案的準確而完整的描述,是一系列解決問題的清晰指令,算法代表著用系統的方法描述解決問題的策略機制。也就是說,能夠對一定規範的輸入,在...
隨機數是專門的隨機試驗的結果。在統計學的不同技術中需要使用隨機數,比如在從統計總體中抽取有代表性的樣本的時候,或者在將實驗動物分配到不同的試驗組的過程中,...
偽隨機數是用確定性的算法計算出來自[0,1]均勻分布的隨機數序列。並不真正的隨機,但具有類似於隨機數的統計特徵,如均勻性、獨立性等。在計算偽隨機數時,若使用...
隨機結構與算法(美)(Random Structures &Algorithms ) ( New York ) 1990年創刊.刊號:513B0076, ISSN1042-9832.美國John Wiley &Sons公司出版、發行.季刊.刊載...
隨機序列(random sequence),也稱隨機數列,全稱隨機變數序列,是由隨機變數組成的數列。它在機率論和統計學中都十分重要。...
隨機並行梯度下降算法(stochastic parallel gradient descent algorithm),簡稱SPGD算法。作為一種無模型最佳化算法,比較適用於控制變數較多,受控系統比較複雜,無法建立準確...
把單個晶片( one chip)內的邏輯元件經過適當組合,實現一定的邏輯電路,稱為隨機邏輯( random logic)。即使簡單的邏輯電路用1個IC晶片也不一定夠,常常要將從數個...
《圖解算法》是2017年9月機械工業出版社出版的圖書,作者是俞征武。...... 修剪與搜尋法、樹搜尋法、問題轉換、圖算法、計算幾何、算法的難題、逼近算法、隨機算法...
軟體測試中除了根據測試用例和測試說明書進行測試外,還需要進行隨機測試(Ad-hoctesting),主要是根據測試者的經驗對軟體進行功能和性能抽查。...
啟發式算法(heuristic algorithm)是相對於最最佳化算法提出的。一個問題的最優算法求得該問題每個實例的最優解。啟發式算法可以這樣定義:一個基於直觀或經驗構造的算法...
“智慧型算法”是指在工程實踐中,經常會接觸到一些比較“新穎”的算法或理論,比如模擬退火,遺傳算法,禁忌搜尋,神經網路等。這些算法或理論都有一些共同的特性(比如...
中央隨機系統是為臨床試驗中隨機化分配、受試者管理、藥品管理等服務所使用到的一種計算機信息系統,功能之一是受試者登記。...
隨機函式就是產生數的函式,是EXCEL中很重要的函式,C語言裡也有rand(),srand()等隨機函式。...
CRF算法,中文名稱條件隨機場算法,外文名稱conditional random field algorithm,是一種數學算法,是2001年提出的,基於遵循馬爾可夫性的機率圖模型。...
隨機遊走(random walk)也稱隨機漫步,隨機行走等是指基於過去的表現,無法預測將來的發展步驟和方向。核心概念是指任何無規則行走者所帶的守恆量都各自對應著一個擴散...
