拉斯維加斯算法不會得到不正確的解。一旦用拉斯維加斯算法找到一個解，這個解就一定是正確解。但有時用拉斯維加斯算法找不到解。與蒙特卡羅算法類似，拉斯維加斯算法找到正確解的機率隨著它所用的計算時間的增加而提高。對於所求解問題的任一實例，用同一拉斯維加斯算法反覆對該實例求解足夠多次，可使求解失敗的機率任意小。
基本介紹
- 中文名：拉斯維加斯算法
- 優點：得到的解一定是正解
- 缺點：有時候找不到解
- 效果：求解失敗的機率小
簡介,算法,隨機化算法,快速排序,
簡介
在電腦運算中，拉斯維加斯算法是一種永遠給出正確解的隨機化算法；也就是說，它總是給出正確結果，或是返回失敗。 換言之，拉斯維加斯算法不賭結果的正確性，而是賭運算所用資源。一個簡單的例子是隨機快速排序，他的中心點雖然是隨機選擇的，但排序結果永遠一致。
算法
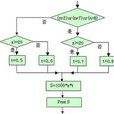
算法如下：
GSAT(Γ∈CNF)
begin
1. for i=1 to Max-tries
2. S=random(Γ); // random assignment
3. for j=1 to Max-moves;
4. if S satisfies Γ then return(Yes);
5. else S=S with some variable flipped to minimize the
number of unsatisfied clauses;
6. end;
7. end;
8. return (No satisfying truth assignment found)
end
隨機化算法
隨機化算法（randomized algorithm），是這樣一種算法，在算法中使用了隨機函式，且隨機函式的返回值直接或者間接的影響了算法的執行流程或執行結果。就是將算法的某一步或某幾步置於運氣的控制之下，即該算法在運行的過程中的某一步或某幾步涉及一個隨機決策，或者說其中的一個決策依賴於某種隨機事件。
快速排序
步驟為：
- 從數列中挑出一個元素，稱為“基準”（pivot），
- 重新排序數列，所有比基準值小的元素擺放在基準前面，所有比基準值大的元素擺在基準後面（相同的數可以到任何一邊）。在這個分割結束之後，該基準就處於數列的中間位置。這個稱為分割（partition）操作。
- 遞歸地（recursively）把小於基準值元素的子數列和大於基準值元素的子數列排序。
遞歸到最底部時，數列的大小是零或一，也就是已經排序好了。這個算法一定會結束，因為在每次的疊代（iteration）中，它至少會把一個元素擺到它最後的位置去。
