基本介紹
- 中文名：遞歸
- 外文名：recursion
- 分類：計算機算法
- 屬性：編程技巧
遞歸定義,遞歸套用,
遞歸定義
遞歸，就是在運行的過程中調用自己。
構成遞歸需具備的條件：
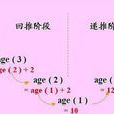
函式嵌套調用過程示例
函式嵌套調用過程示例1. 子問題須與原始問題為同樣的事，且更為簡單；
2. 不能無限制地調用本身，須有個出口，化簡為非遞歸狀況處理。
例如，下列為某人祖先的遞歸定義：
某人的雙親是他的祖先（基本情況）。某人祖先的雙親同樣是某人的祖先（遞歸步驟）。斐波納契數列（Fibonacci Sequence），又稱黃金分割數列，指的是這樣一個數列：1、1、2、3、5、8、13、21..... I
斐波納契數列是典型的遞歸案例：
遞歸關係就是實體自己和自己建立關係。
Fib(0) = 1 [基本情況] Fib(1) = 1 [基本情況] 對所有n > 1的整數：Fib(n) = (Fib(n-1) + Fib(n-2)) [遞歸定義] 儘管有許多數學函式均可以遞歸表示，但在實際套用中，遞歸定義的高開銷往往會讓人望而卻步。例如：
階乘（1) = 1 [基本情況] 對所有n > 1的整數：階乘（n) = (n * 階乘（n-1)) [遞歸定義] 一種便於理解的心理模型，是認為遞歸定義對對象的定義是按照“先前定義的”同類對象來定義的。例如：你怎樣才能移動100個箱子？答案：你首先移動一個箱子，並記下它移動到的位置，然後再去解決較小的問題：你怎樣才能移動99個箱子？最終，你的問題將變為怎樣移動一個箱子，而這時你已經知道該怎么做的。
德羅斯特效應是遞歸的一種視覺形式。圖中女性手持的物體中有一幅她本人手持同一物體的小圖片，進而小圖片中還有更小的一幅她手持同一物體的圖片，依此類推。
德羅斯特效應
德羅斯特效應又例如，我們在兩面相對的鏡子之間放一根正在燃燒的蠟燭，我們會從其中一面鏡子裡看到一根蠟燭，蠟燭後面又有一面鏡子，鏡子裡面又有一根蠟燭……這也是遞歸的表現。
遞歸套用
遞歸算法一般用於解決三類問題：
(1)數據的定義是按遞歸定義的。（Fibonacci函式）
(2)問題解法按遞歸算法實現。
這類問題雖則本身沒有明顯的遞歸結構，但用遞歸求解比疊代求解更簡單，如Hanoi問題。
(3)數據的結構形式是按遞歸定義的。
如二叉樹、廣義表等，由於結構本身固有的遞歸特性，則它們的操作可遞歸地描述。
遞歸的缺點：
遞歸算法解題相對常用的算法如普通循環等，運行效率較低。因此，應該儘量避免使用遞歸，除非沒有更好的算法或者某種特定情況，遞歸更為適合的時候。在遞歸調用的過程當中系統為每一層的返回點、局部量等開闢了棧來存儲。遞歸次數過多容易造成棧溢出等。
遞歸典型問題： 梵塔問題（漢諾塔問題）
已知有三根針分別用A, B, C表示，在A中從上到下依次放n個從小到大的盤子，現要求把所有的盤子
從A針全部移到B針，移動規則是：可以使用C臨時存放盤子，每次只能移動一塊盤子，而且每根針上
不能出現大盤壓小盤，找出移動次數最小的方案.
/*Name:HANOITOWER*Description:solvethehanoitowerproblembyrecursion*/#include<stdio.h>#include<stdlib.h>/*movenplates:from-->to,*thebuffercanbeusedifneeded*/inthanoi(intn,charfrom,charbuffer,charto){ if(n==1) { /*movetheNO.1platedirectly:from-->to*/ printf("Moveplate#%dfrom%cto%c\n",n,from,to); /*theNO.1plateismovedsoreturn*/ return0; } else { /*nplatestobemoved:from-->to, *movethen-1platesabove:from-->buffer, *givethistasktothenextrecursion*/ hanoi(n-1,from,to,buffer); /*then-1platesaboveweremovedtobuffer, *sotheNO.nplatecanbemoveddirectly*/ printf("Moveplate#%dfrom%cto%c\n",n,from,to); /*howeverthen-1platesarestillinbuffer, *movethemtotheterminalposition, *(the"from"positionhasnoplate,&canbeoneso-calledbuffer)*/ hanoi(n-1,buffer,from,to); /*thetaskgivenisdonesoreturn*/ return0; }}intmain(){#defineN4 /*NplatesinA,let'smovethemtoC*/ hanoi(N,'A','B','C'); return0;}如：
//pascalprocedurea;begina;end;
這種方式是直接調用.
又如：
//pascalprocedureb;beginc;end;procedurec;beginb;end;
這種方式是間接調用.
例1計算n!可用遞歸公式如下：
1 當 n=0 時
fac(n)={n*fac(n-1) 當n>0時
可編寫程式如下：
//pascalprogramfac2;varn:integer;functionfac(n:integer):real;beginifn=0thenfac:=1elsefac:=n*fac(n-1)；end;beginwrite('n=');readln(n);writeln('fac(',n,')=',fac(n):6:0);end.例2 樓梯有n階台階，上樓可以一步上1階，也可以一步上2階，編一程式計算共有多少種不同的走法.
設n階台階的走法數為f(n)
顯然有
1 n=1
f(n)={2 n=2
f(n-1)+f(n-2) n>2
可程式序如下：
//pascalprogramlouti;varn:integer;functionf(x:integer):integer;beginifx=1thenf:=1elseifx=2thenf:=2elsef:=f(x-1)+f(x-2);end;beginwrite('n=');read(n);writeln('f(',n,')=',f(n))end.2.2 如何設計遞歸算法
1.確定遞歸公式
2.確定邊界（終了)條件
練習：
用遞歸的方法完成下列問題
1.求數組中的最大數
2.1+2+3+...+n
3.求n個整數的積
4.求n個整數的平均值
5.求n個自然數的最大公約數與最低公倍數
6.有一對雌雄兔，每兩個月就繁殖雌雄各一對兔子.問n個月後共有多少對兔子
7.已知：數列1,1,2,4,7,13,24,44,...求數列的第 n項.
2.3典型例題
例3 快速排序
快速排序的思想是：先從數據序列中選一個元素,並將序列中所有比該元素小的元素都放到它的右邊或左邊，再對左右兩邊分別用同樣的方法處之直到每一個待處理的序列的長度為1,處理結束.
程式如下：
programkspv;vara:array[0..10000]oflongint;i,n:integer;procedurequicksort(l,r:longint);vari,j,mid:longint;begini:=l;j:=r;mid:=a[(l+r)div2];repeatwhilea[i]<middoinc(i);whilea[j]>middodec(j);ifi<=jthenbegina[0]:=a[i];a[i]:=a[j];a[j]:=a[0];inc(i);dec(j);end;untili>j;ifi<rthenquicksort(i,r);ifl<jthenquicksort(l,j);end;beginwrite('inputdata:');readln(n);fori:=1tondoread(a[i]);writeln;quicksort(1,n);write('outputdata:');fori:=1tondowrite(a[i],'');writeln;end.