遞歸做為一種算法在程式設計語言中廣泛套用。是指函式/過程/子程式在運行過程中直接或間接調用自身而產生的重入現象。遞歸是計算機科學的一個重要概念，遞歸的方法是程式設計中有效的方法，採用遞歸編寫程式能使程式變得簡潔和清晰。。
遞歸算法是把問題轉化為規模縮小了的同類問題的子問題。然後遞歸調用函式(或過程)來表示問題的解。
基本介紹
- 中文名：遞歸運算法
- 外文名：Recursive Arithmetic
摘要,定義,算法,套用,實例,網頁中的套用,
摘要
遞歸做為一種算法在程式設計語言中廣泛套用。是指函式/過程/子程式在運行過程中直接或間接調用自身而產生的重入現象。遞歸是計算機科學的一個重要概念，遞歸的方法是程式設計中有效的方法，採用遞歸編寫程式能使程式變得簡潔和清晰。。
圖片
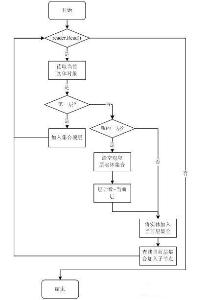
圖片遞歸算法是把問題轉化為規模縮小了的同類問題的子問題。然後遞歸調用函式(或過程)來表示問題的解。
定義
程式調用自身的編程技巧稱為遞歸（ recursion）。
一個過程或函式在其定義或說明中有直接或間接調用自身的一種方法，它通常把一個大型複雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解，遞歸策略只需少量的程式就可描述出解題過程所需要的多次重複計算，大大地減少了程式的代碼量。
遞歸的能力在於用有限的語句來定義對象的無限集合。一般來說，遞歸需要有邊界條件、遞歸前進段和遞歸返回段。當邊界條件不滿足時，遞歸前進；當邊界條件滿足時，遞歸返回。
注意：
(1) 遞歸就是在過程或函數裡調用自身；
(2) 在使用遞歸策略時，必須有一個明確的遞歸結束條件，稱為遞歸出口。
遞歸的另一種定義：
遞歸，就是用自己的簡單情況，定義自己。
在數學和計算機科學中，遞歸指由一種（或多種）簡單的基本情況定義的一類對象或方法，並規定其他所有情況都能被還原為其基本情況。
斐波那契數列是典型的遞歸案例：Fib(0) = 0 [基本情況] Fib(1) = 1 [基本情況] 對所有n > 1的整數：Fib(n) = (Fib(n-1) + Fib(n-2)) [遞歸定義] 儘管有許多數學函式均可以遞歸表示，但在實際套用中，遞歸定義的高開銷往往會讓人望而卻步。
例如：階乘（1) = 1 [基本情況] 對所有n > 1的整數：階乘（n) = (n * 階乘（n-1)) [遞歸定義] 一種便於理解的心理模型，是認為遞歸定義對對象的定義是按照“先前定義的”同類對象來定義的。
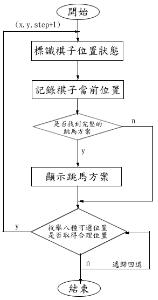
例如：你怎樣才能移動100個箱子？答案：你首先移動一個箱子，並記下它移動到的位置，然後再去解決較小的問題：你怎樣才能移動99個箱子？最終，你的問題將變為怎樣移動一個箱子，而這是你已經知道該怎么做的。
如此的定義在數學中十分常見。例如，集合論對自然數的正式定義是：1是一個自然數，每個自然數都有一個後繼，這一個後繼也是自然數。
算法
遞歸過程一般通過函式或子過程來實現。遞歸算法：在函式或子過程的內部，直接或者間接地調用自己的算法。
遞歸算法的特點
遞歸算法是一種直接或者間接地調用自身的算法。在計算機編寫程式中，遞歸算法對解決一大類問題是十分有效的，它往往使算法的描述簡潔而且易於理解。
遞歸算法是一種直接或者間接地調用自身的算法。在計算機編寫程式中，遞歸算法對解決一大類問題是十分有效的，它往往使算法的描述簡潔而且易於理解。
遞歸算法解決問題的特點：
(1) 遞歸就是在過程或函數裡調用自身。
(2) 在使用遞歸策略時，必須有一個明確的遞歸結束條件，稱為遞歸出口。
(3) 遞歸算法解題通常顯得很簡潔，但遞歸算法解題的運行效率較低。所以一般不提倡用遞歸算法設計程式。
(4) 在遞歸調用的過程當中系統為每一層的返回點、局部量等開闢了棧來存儲。遞歸次數過多容易造成棧溢出等。所以一般不提倡用遞歸算法設計程式。
遞歸算法要求
遞歸算法所體現的“重複”一般有三個要求：
遞歸算法要求
遞歸算法所體現的“重複”一般有三個要求：
一是每次調用在規模上都有所縮小(通常是減半)；
二是相鄰兩次重複之間有緊密的聯繫，前一次要為後一次做準備(通常前一次的輸出就作為後一次的輸入)；
三是在問題的規模極小時必須用直接給出解答而不再進行遞歸調用，因而每次遞歸調用都是有條件的(以規模未達到直接解答的大小為條件)，無條件遞歸調用將會成為死循環而不能正常結束。
套用
遞歸算法一般用於解決三類問題：
(1)數據的定義是按遞歸定義的。（Fibonacci函式）
(2)問題解法按遞歸算法實現。（回溯）
(3)數據的結構形式是按遞歸定義的。（樹的遍歷，圖的搜尋）
遞歸的缺點： 遞歸算法解題相對常用的算法如普通循環等，運行效率較低。因此，應該儘量避免使用遞歸，除非沒有更好的算法或者某種特定情況，遞歸更為適合的時候。在遞歸調用的過程當中系統為每一層的返回點、局部量等開闢了棧來存儲。遞歸次數過多容易造成棧溢出等。
實例
比如：運用遞歸算法查詢多個上下級關係樹的數據結構中的數據（C# 語法）
圖片privateviod GET()
{
int Count= 0;
Count = GetCount(1,ProductCount);
}
private int GetCount(int ParentID, int ProductCount)
{
string sqlString = "SELECT* FROM表 WHERE ID=" + ParentID;
Model model = BLL.GetModel(sqlString); //BLL.GetModel()是自定義方法
if(model != null) //條件
{
Count += model.Count;
GetCount(model.ID,Count); //遞歸
}
else
{
return Count;
}
//備註：當遞歸查詢完所有的上下級關係樹，該遞歸才會結束，才會返回Count
}
網頁中的套用
在網站開發中，遞歸算法大量套用於無限級分類
