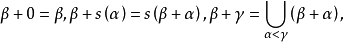超限遞歸定理(transfinite recursive theorem)是遞歸定理的推廣，該定理斷言：對任意函式F：V→V，存在惟一的函式G：ord→V，使得對任意α∈ord有G(α)=F(G|α)，這裡V表示一切集合構成的類，G|α表示函式G在α上的限制。當在上述定理限於考慮函式G：ω→V這一特殊情形時，定理就變成平常的遞歸定理。超限遞歸定理是馮·諾伊曼(J.von Neumann)於1923年提出的，該定理的意義是，由已給的函式F，以集合{G(β)|β<α}為F的自變數，所確定的函式值作為被定義函式G在α上的值，所定義出的函式G是惟一確定的，這種定義函式的方法不同於一般的定義方法，因為在定義G(α)時要用到已給的F，而且要用到各個G(β)，β<α。
基本介紹
- 中文名：超限遞歸定理
- 外文名：transfinite recursive theorem
- 所屬學科：數學（集合論）
- 所屬問題：樸素集合論（序數）
- 簡介：研究超限無窮集合的主要基礎
- 提出者：馮·諾伊曼(J.von Neumann)
基本介紹,相關說明,
基本介紹
超限遞歸定理 對於每一個公式γ(x，y)有下述定理：設(A，<)為良序集，且對任何f有唯一的y使γ(f，y)成立，則存在唯一以A為定義域的函式F，使得對於A中的所有t，有：
γ(F↾Seg t，F(t))，
其中 Seg t={x|x<t∧x∈A}。
這是個定理模式，表明有無限多個定理，對於每一個γ(x，y)，它都是一個定理。
相關說明
有了良序集，便可在其上建立兩個重要的定理，即超限歸納定理和超限遞歸定理，它們是研究超限無窮集合的主要基礎。所謂超限無窮集合是指超過自然數集合ω的任何無窮集合，由於ω是第一非有限的、最小的無窮集合，是第一個遇到的極限序數，超過這個極限序數的無窮集合論證問題都屬於超限問題，歸納定理的主要功能是克服了無窮元都要論證的困難。而遞歸定理的主要功能是確立運算函式的存在，給出計數的特性，以及其它論證中的作用。
在定義序數運算（加、乘、冪）時，需要用超限遞歸定理：若G是一運算，則有一運算F，使得對每一序數α，都有F(α)=G(F↾α)。而這一定理的證明要用到代換公理。有了代換公理還可以得到極限序數ω+ω的存在性。如果先將正整數從小排到大，再把非正整數從大排到小而成一序列：1，2，3，…，0，-1，-2，…。從而全體整數就良序了，其序型即為ω+ω。
事實上，任一良序集<ω，<>，都有唯一的序數α使得<ω，<>序同構於<α，∈>。因此，就可以把良序集按序同構來分類，並將同屬於一類的稱為具有同一序型的良序集。而序數就可定義作為同構的良序集的代表。依此，可以定義序數的運算。例如，序數的加法可以定義如下：若α,β為序數，γ為極限序數。
超限遞歸定理的證明需要套用下面的代換公理。
代換公理對於任何集合A和一個具有函式性質且不含B的公式φ(x，y)有：
或完全形式地表示為：
(∀A)((∀x)(∃!y)(x∈A^φ(x，y)→(∃B)(∀y)(y∈B⇆(∃x)(x∈∧φ(x，y))))。
如果把φ(x，y)理解為“x被代換成y”，代換公理可表述成：若A的每個元至多被代換一個對象，則所有被代換的對象就構成了一個集合B。
