基本介紹
- 中文名：序數加法
- 外文名：addition of ordinals
- 所屬學科：數學（集合論）
- 所屬問題：序數
- 簡介：序數的一種運算
定義,序數加法的運算性質,相關說明,
定義
序數的加法可以定義如下：若α,β為序數，γ為極限序數。
序數加法的運算性質
序數加法不滿足交換律，如1+ω=ω+≠ω=ω+1。數加法有下列性質：對任意序數α，β，γ有：
1.α+(β+γ)=(α+β)+γ.
2.α+β=α+γ
β=γ.
3.α+β<α+γβ<γ.
4.α<β
α+γ≤β+γ.
5.α+γ<βγα<β.
相關說明
如果一集合x的元素的元素也都還是x的元素，則稱x為傳遞集。一個集合x是自然數：如果x是傳遞集，x的全體元素在∈下良序，而且x的每一非空子集對序∈而言有最大元。這樣可以把自然數變成了在ZF內可以定義的一種性質，如把0定義作空集∅，1定義作0U{0}，2定義作1U{1}，……等等，則0，1，2，…，都是自然數，而且只有這些是自然數。
序數是自然數的推廣。
“x是序數”是指如果集合x是傳遞集，而且x在∈下良序。令On表示全體序數所成的集合，α,β∈On，α<β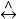
α∈β。這樣，就用∈定義了序數間的<關係，每一序數都是由比它自身小的序數所組成的集合。
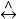
每一自然數都是序數，全體自然數也是序數。對任一集合x，令s(x)=xU{x}。則當x是序數時，s(x)亦為序數。一序數α稱作後繼序數：如果有一序數β，使α=s(β)。不是後繼序數的序數稱為極限序數。例如0，ω均為極限序數。
On雖為一真類，但<On，<>具有性質：On的任一非空子類都有最小元。因此，要想證明每一序數都具有性質妒，即可套用超限歸納原理：對於任給的一序數B，若每一比8小的序數a都具有性質妒則母亦具有性質9，那么對所有的序數都具有性質φ。
在定義序數運算（加、乘、冪）時，需要用超限遞歸定理：若G是一運算，則有一運算F，使得對每一序數α，都有F(α)=G(F↾α)。而這一定理的證明要用到代換公理。有了代換公理還可以得到極限序數ω+ω的存在性。如果先將正整數從小排到大，再把非正整數從大排到小而成一序列：1，2，3，…，0，-1，-2，…。從而全體整數就良序了，其序型即為ω+ω。
事實上，任一良序集<ω，<>，都有唯一的序數α使得<ω，<>序同構於<α，∈>。因此，就可以把良序集按序同構來分類，並將同屬於一類的稱為具有同一序型的良序集。而序數就可定義作為同構的良序集的代表。依此，可以定義序數的運算。例如，序數的加法可以定義如下：若α,β為序數，γ為極限序數。
