基本介紹
- 中文名:廣度優先算法
- 外文名:Breadth-First Search
- 詞性:名詞
- 範疇:數學;計算機科學
思想
實現

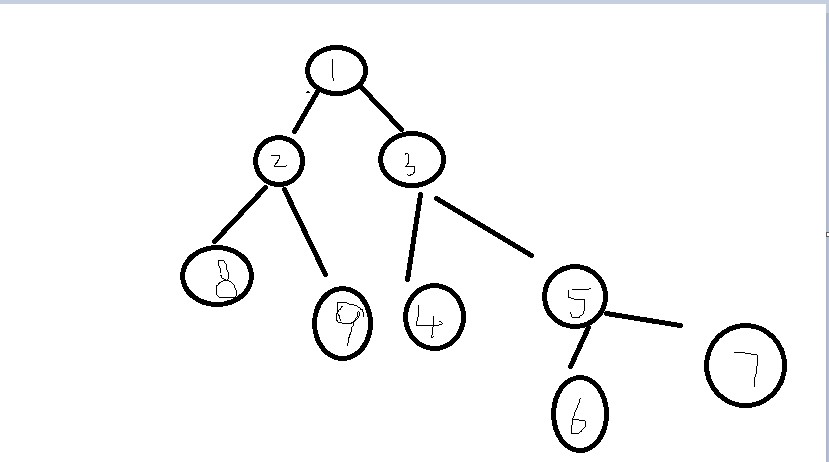

廣度優先算法(Breadth-First Search),同廣度優先搜尋,又稱作寬度優先搜尋,或橫向優先搜尋,簡稱BFS,是一種圖形搜尋演算法。簡單的說,BFS是從根節點開始,沿著樹的...
深度優先算法,是電腦程式的一種編制原理,就是在一個問題出現多種可以實現的方法和技術的時候,應該優先選擇哪個更合適的,也是一種普遍的邏輯思想,此種思想在運算...
廣度優先遍歷是連通圖的一種遍歷策略。因為它的思想是從一個頂點V0開始,輻射狀地優先遍歷其周圍較廣的區域,故得名。...
寬度優先搜尋算法(又稱廣度優先搜尋)是最簡便的圖的搜尋算法之一,這一算法也是很多重要的圖的算法的原型。Dijkstra單源最短路徑算法和Prim最小生成樹算法都採用了...
搜尋算法是利用計算機的高性能來有目的的窮舉一個問題解空間的部分或所有的可能情況,從而求出問題的解的一種方法。現階段一般有枚舉算法、深度優先搜尋、廣度優先...
在搜尋算法中,深度優先搜尋(也可以稱為回溯法)是搜尋算法里最簡單也最常見的,今天我們就從這裡講起,下面的內容假設讀者已經知道最基本的程式設計和簡單的遞歸算法...
常用的基礎算法有快速排序算法、堆排序算法、歸併排序、二分查找算法、BFPRT(線性查找算法)、DFS(深度優先搜尋)、BFS(廣度優先搜尋)、Dijkstra算法、動態規劃算法、...
我們說套用這種估價函式的最好優先算法就是A*算法。舉一個例子,其實廣度優先算法就是A*算法的特例。其中g(n)是節點所在的層數,h(n)=0,這種h(n)肯定小於h'...
在這個搜尋策略中,一個具有深度限制的深度優先搜尋算法會不斷重複地運行,並且同時放寬對於搜尋深度的限制,直到找到目標狀態。IDDFS 與廣度優先算法是等價的,但對記憶體...
廣度優先是從初始狀態一層一層向下找,直到找到目標為止。深度優先是按照一定的順序前查找完一個分支,再查找另一個分支,以至找到目標為止。這兩種算法在數據結構書中...
當再次搜尋到這個重複節點時,由於套用的算符基本一致,還會產生重複,所以為了節約時間和存儲空間,往往在深度優先算法中設立一個機制,用來刪除這些重複的節點,以提高...
《算法(第4版)》是一本美 Robert Sedgewick / 美Kevin Wayne編寫,由人民郵電...4.1.5 廣度優先搜尋 344 4.1.6 連通分量 349 4.1.7 符號圖 352 4.1.8 總結...
《算法之道》既可以作為大學本科或研究生的算法教材或參考書,也可以作為對算法有興趣的讀者提升認知深度的讀物。算法之道內容簡介 編輯 《算法之道》追求的目標是...
這種以深度優先的方式系統地搜尋問題的解的算法稱為回溯法,它適用於解一些組合數較大的問題。回溯算法算法框架 編輯 (pascal語言)procedure try(i:integer); var ...
《算法分析與設計》是由人民郵電出版社於2006年10月出版的圖書,作者是古德里奇、...6.3.3 廣度優先查找6.4 有向圖6.4.1 遍歷有向圖6.4.2 傳遞閉包...
介《啊哈!算法》中涉及的數據結構有棧、佇列、鍊表、樹、並查集、堆和圖等;涉及的算法有排序、枚舉、深度和廣度優先搜尋、圖的遍歷,當然還有圖論中不可以缺少的...
先驗算法採用廣度優先搜尋算法進行搜尋並採用樹結構來對候選項目集進行高效計數。它通過長度為k− 1的候選項目集來產生長度為k的候選項目集,然後從中刪除包含不...
5.2貪心算法及其套用5.3習題第6章動態規劃6.1動態規劃的原理6.2動態規劃的套用6.3背包問題6.4習題第7章搜尋7.1枚舉7.2深度優先搜尋...
警用算法導論:倒退一步67第十章 用廣度優先搜尋去開鎖69搜尋第五站:Frayed Cable島,這裡有一座廢棄的監獄,Socks用咒語打開了監獄大門的鎖。警用算法導論:廣度優先...
廣度優先搜尋策略是指在抓取過程中,在完成當前層次的搜尋後,才進行下一層次的搜尋。該算法的設計和實現相對簡單。在目前為覆蓋儘可能多的網頁,一般使用廣度優先搜尋...
