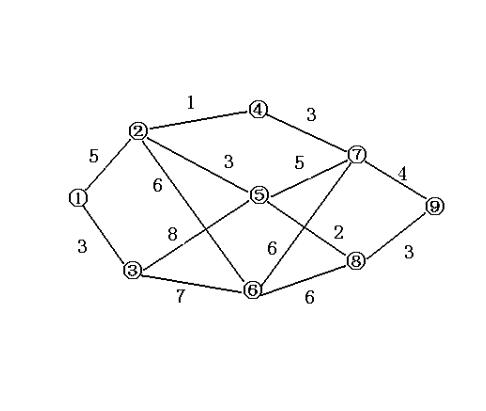
用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優解，但由於它遍歷計算的節點很多，所以效率低。
基本介紹
- 中文名：最短路徑
- 外文名：shortest path
- 性質：一類經典算法問題
- 解決思路：由已知點/邊向外擴展
- 解決方法：SPFA算法、Dijkstra算法等
最短路徑介紹,解決方法,最短路徑算法,
最短路徑介紹
最短路徑問題是圖論研究中的一個經典算法問題， 旨在尋找圖（由結點和路徑組成的）中兩結點之間的最短路徑。 算法具體的形式包括：
確定起點的最短路徑問題 - 即已知起始結點，求最短路徑的問題。
確定終點的最短路徑問題 - 與確定起點的問題相反，該問題是已知終結結點，求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同，在有向圖中該問題等同於把所有路徑方向反轉的確定起點的問題。
確定起點終點的最短路徑問題 - 即已知起點和終點，求兩結點之間的最短路徑。
全局最短路徑問題 - 求圖中所有的最短路徑。
解決方法
綜述
用於解決最短路徑問題的算法被稱做“最短路徑算法”， 有時被簡稱作“路徑算法”。 最常用的路徑算法有：
Johnson算法
所謂單源最短路徑問題是指：已知圖G=（V，E），我們希望找出從某給定的源結點S∈V到V中的每個結點的最短路徑。
首先，我們可以發現有這樣一個事實：如果P是G中從vs到vj的最短路，vi是P中的一個點，那么，從vs沿P到vi的路是從vs到vi的最短路。
最短路徑算法
Dijkstra算法（迪傑斯特拉）是典型的最短路徑路由算法，用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優解，但由於它遍歷計算的節點很多，所以效率低。可以用堆最佳化。
Dijkstra算法是很有代表性的最短路算法，在很多專業課程中都作為基本內容有詳細的介紹，如數據結構，圖論，運籌學等等。
Dijkstra一般的表述通常有兩種方式，一種用永久和臨時標號方式，一種是用OPEN, CLOSE表方式，Drew為了和下面要介紹的 A* 算法和 D* 算法表述一致，這裡均採用OPEN,CLOSE表的方式。
其採用的是貪心法的算法策略
大概過程：
創建兩個表，OPEN, CLOSE。
OPEN表保存所有已生成而未考察的節點，CLOSED表中記錄已訪問過的節點。
1． 訪問路網中距離起始點最近且沒有被檢查過的點，把這個點放入OPEN組中等待檢查。
2． 從OPEN表中找出距起始點最近的點，找出這個點的所有子節點，把這個點放到CLOSE表中。
3． 遍歷考察這個點的子節點。求出這些子節點距起始點的距離值，放子節點到OPEN表中。
4． 重複第2和第3步,直到OPEN表為空，或找到目標點。
C++代碼
#include<iostream>#include<vector>using namespace std;void dijkstra(const int &beg,//出發點 const vector<vector<int> > &adjmap,//鄰接矩陣，通過傳引用避免拷貝 vector<int> &dist,//出發點到各點的最短路徑長度 vector<int> &path)//路徑上到達該點的前一個點//負邊被認作不聯通//福利：這個函式沒有用任何全局量，可以直接複製！{ const int &NODE=adjmap.size();//用鄰接矩陣的大小傳遞頂點個數，減少參數傳遞 dist.assign(NODE,-1);//初始化距離為未知 path.assign(NODE,-1);//初始化路徑為未知 vector<bool> flag(NODE,0);//標誌數組，判斷是否處理過 dist[beg]=0;//出發點到自身路徑長度為0 while(1) { int v=-1;//初始化為未知 for(int i=0; i!=NODE; ++i) if(!flag[i]&&dist[i]>=0)//尋找未被處理過且 if(v<0||dist[i]<dist[v])//距離最小的點 v=i; if(v<0)return;//所有聯通的點都被處理過 flag[v]=1;//標記 for(int i=0; i!=NODE; ++i) if(adjmap[v][i]>=0)//有聯通路徑且 if(dist[i]<0||dist[v]+adjmap[v][i]<dist[i])//不滿足三角不等式 { dist[i]=dist[v]+adjmap[v][i];//更新 path[i]=v;//記錄路徑 } }}int main(){ int n_num,e_num,beg;//含義見下 cout<<"輸入點數、邊數、出發點："; cin>>n_num>>e_num>>beg; vector<vector<int> > adjmap(n_num,vector<int>(n_num,-1));//默認初始化鄰接矩陣 for(int i=0,p,q; i!=e_num; ++i) { cout<<"輸入第"<<i+1<<"條邊的起點、終點、長度（負值代表不聯通）："; cin>>p>>q; cin>>adjmap[p][q]; } vector<int> dist,path;//用於接收最短路徑長度及路徑各點 dijkstra(beg,adjmap,dist,path); for(int i=0; i!=n_num; ++i) { cout<<beg<<"到"<<i<<"的最短距離為"<<dist[i]<<"，反向列印路徑："; for(int w=i; path[w]>=0; w=path[w]) cout<<w<<"<-"; cout<<beg<<'\n'; }}