在數學領域,函式是一種關係,這種關係使一個集合里的每一個元素對應到另一個(可能相同的)集合里的唯一元素。
基本介紹
- 中文名:數學函式
簡介
函式定義
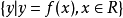
函式相關概念
幾何含義
函式的集合論(關係)定義
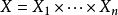
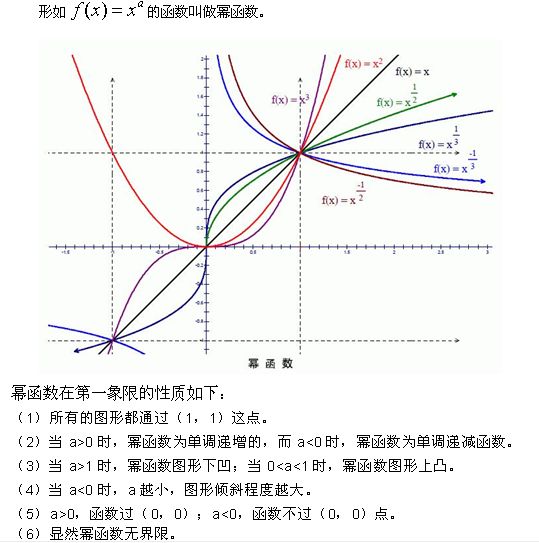
在數學領域,函式是一種關係,這種關係使一個集合里的每一個元素對應到另一個(可能相同的)集合里的唯一元素。
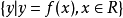
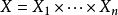
在數學領域,函式是一種關係,這種關係使一個集合里的每一個元素對應到另一個(可能相同的)集合里的唯一元素。...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
函式的定義:給定一個數集A,對A施加對應法則f,記作f(A),得到另一數集B,也就是B=f(A)。那么這個關係式就叫函式關係式,簡稱函式。函式概念含有三個要素:定義...
數學公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
sign又叫sgn,意思是符號。符號函式(一般用sign(x)表示)是很有用的一類函式,能夠幫助我們在幾何畫板中實現一些直接實現有困難的構造。 符號函式 能夠把函式的符號...
計算機程式語言的一種函式,主要套用數據運算。Math函式可以被套用於解決部分電腦程式問題...
三角函式是數學中屬於初等函式中的超越函式的函式。它們的本質是任何角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的。其定義...
萬能公式包括三角函式、反三角函式等。萬能公式,可以把所有三角函式都化成只有tan(a/2)的多項式。將sinα、cosα、tanα代換成含有tan(α/2)的式子,這種代換稱...
不是初等函式的函式,稱為非初等函式,如狄利克雷函式和黎曼函式。目前有兩種分類方法:數學分析有六種基本初等函式,高等數學只有五種。...
初等函式是由冪函式(power function)、指數函式(exponential function)、對數函式(logarithmic function)、三角函式(trigonometric function)、反三角函式(inverse ...
約翰.伯努利於1694年首次提出函式(function)概念,並以字母 n 表示變數 z 的一個函式;至 1697年,他又以大寫字母 X 及相應之希臘字母 ξ表示變數 x 的函式。...
在數學里,線性函式是指那些線性的函式,但也常用作一次函式的別稱,儘管一次函式不一定是線性的。線型函式是一個比較恰當的同義詞。...
值域:數學名詞,函式經典定義中,因變數改變而改變的取值範圍叫做這個函式的值域,在函式現代定義中是指定義域中所有元素在某個對應法則下對應的所有的象所組成的集合...
數學符號的發明及使用比數字要晚,但其數量卻超過了數字。現代數學常用的數學符號已超過了200個,其中,每一個符號都有一段有趣的經歷。...
sinx函式,即正弦函式,三角函式的一種。正弦函式是三角函式的一種。對於任意一個實數x都對應著唯一的角(弧度制中等於這個實數),而這個角又對應著唯一確定的正弦值...
《輕鬆搞定高中數學:函式》倒數第一的學生考上了北大、他讓準備放棄高考的學生成為理科狀元、他的一個班有37人被北大、清華錄取、另有10人被牛津、劍橋、耶魯等...
《國中數學》是2009年11月由北京師範大學出版社出版的圖書,作者是吳江媛。...... 數學活動小結複習題25第二十六章反比例函式26.1反比例函式信息技術套用探索反比例...
一般地,對數函式以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax=N(a>0,且a≠1),那么數x...
三角函式是數學中屬於初等函式中的超越函式的一類函式。它們的本質是任意角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的,其...
《函式:高中數學(新課標)》由龍門書局出版。龍門品牌,學子至愛。 1 ...... 《函式:高中數學(新課標)》由龍門書局出版。龍門品牌,學子至愛。[1] ...
英文詞,理解為:古代的一種貴族稱號;或者是一種電腦計算機內部的數學函式的名字。...... 英文詞,理解為:古代的一種貴族稱號;或者是一種電腦計算機內部的數學函式的...
《國中數學:函式》是2009年北京教育出版出版的一本圖書。本書針對各考點精選了大量帶有梯度的訓練題,通過練習掌握考點知識。針對本知識專題的特性,精選一批有一定難度...
《國中數學函式及其圖象》是2010年龍門書局出版的圖書,作者是余夢。...... 《國中數學函式及其圖象》是2010年龍門書局出版的圖書,作者是余夢。作者 余夢 ISBN ...
