基本介紹
- 中文名:非空集合
- 外文名:nonempty set
- 所屬領域:集合論
- 定義:至少含有一個元素的集合
- 舉例:除了空集外的其餘集合
定義

相關概念
集合
集合的元素
元素和集合的關係


集合的表示法
 圖 1
圖 1有限集
無限集
空集


單元素集
子集

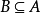

真子集


相等集




交集
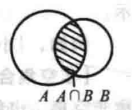 圖 2
圖 2

 圖3
圖3並集
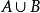
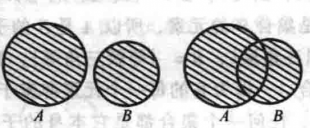 圖4
圖4
 圖5
圖5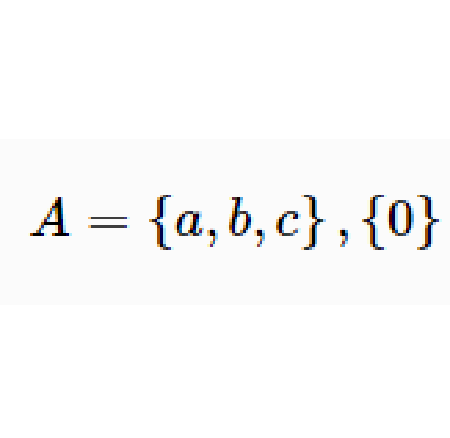



 圖 1
圖 1


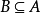







 圖 2
圖 2

 圖3
圖3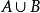
 圖4
圖4
 圖5
圖5在集合論里,至少含有一個元素的集合,叫做非空集合,簡稱非空集。也就是說,除了空集外,其餘的集合都是非空集。...
非空有限集有限集 數學中,一個集合被稱為有限集合,簡單來說就是元素個數有限,嚴格而言則是指有一個自然數n使該集合與集合{1,2,...,n}之間存在雙射。例如...
空集是指不含任何元素的集合。空集是任何集合的子集,是任何非空集合的真子集。空集不是無;它是內部沒有元素的集合。可以將集合想像成一個裝有元素的袋子,而...
有一類特殊的集合,它不包含任何元素,如{x|x∈R x²+1=0} ,稱之為空集,記為∅。空集是個特殊的集合,它有2個特點:空集∅是任意一個非空集合的真...
集合超積概念 編輯 集合超積(ultraproduct of sets)是由一個集合族構成的集合。設I為一非空集合,D是I上一個真濾子,Ai(i∈I)為一族非空集合。令C={f:f...
無限集合(infinite set)亦稱無窮集合,是一類特殊的集合,它有下面幾種定義:1.不是有限集的集合;2.可與其真子集對等的非空集合;3.既不是空集,又不與Mn={1,...
至少有一個結點的二叉樹叫做非空二叉樹。二叉樹是每個節點最多有兩個子樹的樹結構。樹是由n(n>=1)個有限節點組成一個具有層次關係的集合。它具有以下的特點:...
設R是非空集合A上的一個二元關係,若R滿足: 自反性、反對稱性、傳遞性,則稱R為A上的偏序關係。以下為定義:非嚴格偏序,自反偏序...
空關係是一種特殊關係,指關係集A×B中的子集∅。非空集合中的空關係是反自反的、對稱的、反對稱的和傳遞的,但不是自反的;空集合中的空關係則是自反的、反...
任何一組凸集合的集合本身都是凸的,所以(實數或複合)向量空間的凸子集形成一個完整的格線。閔可夫斯基加法在實際向量空間中,將兩個(非空)集合S1和S2的閔可夫...
六、假設非空集合A中含有n個元素,則有:A的子集個數為2n。 A的真子集的個數為2n-1。 A的非空子集的個數為2n-1 A的非空真子集的個數為2n-2。[3...
所謂兩個凸集分離,直觀地看是指兩個凸集合沒有交叉和重合的部分,因此可以用一張超平面將兩者隔在兩邊。設 為兩個非空集合,如果存在非零向量 及 使得則稱超...
空集是任何非空集合的真子集。非空真子集:如果集合A⊊B,且集合A≠∅,集合A是集合B的非空真子集(nonvoid proper subset)。 [2] ...
封閉性,又稱閉包。數學裡,給定一個非空集合S 和一個函式F : S X S -> S ,則稱 F 為在 S 上之二元運算(binary operation),或稱 (S,F) 具有封閉性...
商集是集合論的基本概念之一,指由集合和該集合上的等價關係導出的集合。設~是非空集合A的一個等價關係,若把以A關於~的全部等價類作為元素組成一個新的集合B...
設W為向量空間 V 的一個非空子集,若W在 V 的加法及標量乘法下是封閉的,且零向量0∈ W,就稱W為 V 的線性子空間。給出一個向量集合 B,那么包含它的最...
設𝒜 為一非空集合族,把集合 {x | 𝒜 } 稱為𝒜 所含的元素集合的交集,記為 ∩𝒜。集合的交運算具有下列性質:1、交換律: ...
A X B={(a,b)|a屬於A且b屬於 B} ,則AXB所形成的集合就叫笛卡爾集。設A、B是兩個非空集合,任給x∈A,y∈B,將它們組成一個有序對(x,y),把這種有...
