空關係是一種特殊關係,指關係集A×B中的子集∅。非空集合中的空關係是反自反的、對稱的、反對稱的和傳遞的,但不是自反的;空集合中的空關係則是自反的、反自反的、對稱的、反對稱的和傳遞的。非空集合的空關係的矩陣各元素都是0。
基本介紹
- 中文名:空關係
- 外文名: empty relation
- 所屬學科:離散數學
- 符號表示:∅
- 相關概念:二元關係、全關係、反自反性等
定義










例題解析
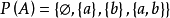


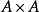



二元關係的性質


空關係是一種特殊關係,指關係集A×B中的子集∅。非空集合中的空關係是反自反的、對稱的、反對稱的和傳遞的,但不是自反的;空集合中的空關係則是自反的、反自反的、對稱的、反對稱的和傳遞的。非空集合的空關係的矩陣各元素都是0。










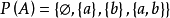


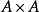




空關係是一種特殊關係,指關係集A×B中的子集∅。非空集合中的空關係是反自反的、對稱的、反對稱的和傳遞的,但不是自反的;空集合中的空關係則是自反的、反...
地緣關係是指以地理位置為聯結紐帶,由於在一定的地理範圍內共同生活、活動而交往產生的人際關係。如同鄉關係、鄰里關係。故土觀念、鄉親觀念就是這種關係的反映。現代...
數學上,二元關係用於討論兩個數學對象的聯繫。諸如算術中的「大於」及「等於」,幾何學中的"相似",或集合論中的"為...之元素"或"為...之子集"。二元關係有...
質量公理分為總體分理和質空關係分理兩部份。1、總體分理:m∈(0,+ ∞)為“無限”,指“宇宙的總質量無限大”。總質量無限大是質量本性。這裡m為靜質量。...
哲學上,空間和時間的依存關係表達著事物的演化秩序。時、空都是絕對概念,是存在的基本屬性。但其測量數值卻是相對於參照系而言的。“時間”內涵是無盡永前;外延是...
質量公理分為總體分理和質空關係分理兩部份。1、總體分理:m∈(0,+ ∞)為“無限”,指“宇宙的總質量無限大”。總質量無限大是質量本性。這裡m為靜質量。...
2、質空關係分理:(dρ)_η≠(dρ)_0為“永有”,指“永不均勻地布滿空間”。“宇宙空間內的任何部份都充滿著質量,不存在不含質量的純空,但各點的微密度...
雖然名字一樣但是和《貓和老鼠》沒有一毛關係的刑天的腦袋,自成一體,全名湯姆·萊昂納多·德華·彥祖,顏值頗高,然而各方面都與身體畫風極度不符合。與黃帝一戰後...
(3)表現時空語義:時空語義包括地理實體的空間結構、有效時間結構、空間關係、時態關係、地理事件、時空關係。時空數據模型指導思想 編輯 (1)根據套用領域的特點(如...
質量公理分為總體分理和質空關係分理兩部份。1、總體分理:m∈(0,+ ∞)為“無限”,指“宇宙的總質量無限大”。總質量無限大是質量本性。這裡m為靜質量。...
2008年6月發射升空。這台世界上最強大的望遠鏡是通過高能伽馬射線觀察宇宙,最初...許多試圖證明萬有引力理論的努力都將時空關係描繪成一種飄忽不定的空洞結構,在...
質量公理分為總體分理和質空關係分理兩部份。1、總體分理:m∈(0,+ ∞)為“無限”,指“宇宙的總質量無限大”。總質量無限大是質量本性。這裡m為靜質量。...
