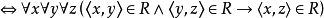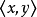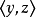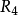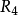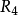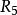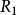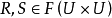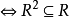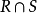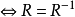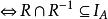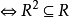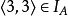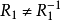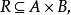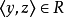傳遞關係

傳遞關係(transitive relation)是一種特殊的關係，指由甲、乙和乙、丙都有，可推知甲、丙也有的那種關係。集合A上的二元關係R，對任何a，b，c∈A，當aRb，bRc時，有aRc，用符號表示：R是A上的傳遞關係⇔∀a∀b∀c(a∈A∧b∈A∧c∈A∧aRb∧bRc→aRc)。當A上的R是傳遞關係時，稱R在A上是傳遞的，或說A上的關係R有傳遞性。例如，實數集中的小於關係與不小於關係都是傳遞的；而人群中的同學關係是不傳遞的。若R在A上是傳遞的，則R_°R⊆R；反之，如R_°R⊆R，則R在A上是傳遞的。一個反自反的傳遞關係是不對稱的，一個反自反的對稱非空關係不是傳遞關係。

基本介紹

• 中文名：傳遞關係
• 外文名：transitive relation
• 所屬學科：數學
• 所屬問題：集合論(關係)
• 相關概念：二元關係，自反關係等

基本介紹

定義

令R是A上的二元關係，對於A中任意的 ，若 ，且 ，則 ，則稱R具有傳遞性(或稱R是傳遞關係)。

R是A上的傳遞關係 。

例題解析

【例1】設A={1，2，3，4}，下列幾個是A 上的二元關係。

R₁={<1，1>，<1，2>，<2，1>，<2，2>，<3，4>，<4，1>，<4，4>}；

R₂={<1，1>，<1，2>，<2，1>}；

R₃={<1，1>，<1，2>，<1，4>，<2，1>，<2，2>，<3，3>，<4，1>，<4，4>}；

R₄={<2，1>，<3，1>，<3，2>，<4，1>，<4，2>，<4，3>}；

R₅=(<1，1>，<1，2>，<1，3>，<1，4>，<2，2>，<2，3>，<2，4>，<3，3>，<3，4>，<4，4>}；

R₆={<3，4>}。

其中，哪些是傳遞關係?

解： 是傳遞的。對這些關係可以證明，若 和 屬於一個關係，則 也屬於這個關係，例如 傳遞的，因為 中只有<3，2>和<2，1>，<4，2>和<2，1>，<4，3>和<3，1>以及<4，3>和<3，2>是這樣的有序對，而<3，1>，<4，1>和<4，2>屬於。

同理可證是傳遞的。

雖然只有一個序對，但它沒有違反傳遞性的規則，故也是傳遞的。

不是傳遞的。因為，。

不是傳遞的，因為而。

不是傳遞的，因為，而。

傳遞關係在關係圖上特徵表現為如果結點u到v有邊，v到w有邊，則必有從u到w的邊。

傳遞關係的性質

設，則有：

(1)若是傳遞的。則。

(2)若是傳遞的，則是傳遞的。

(3)若是傳遞的，則是傳遞的。

關係的判斷

綜上所述。判斷一個A上的二元關係具有哪些性質。可以從定義出發，或者觀察關係的關係圖和關係矩陣。對於一些簡單的特徵明顯的關係是容易判斷的，然而如何判斷任意一個關係具有哪些性質呢?下面給出判斷的形式化表示。

定理1 設R是A上的二元關係，則

(1) R是自反關係。

(2) R是反自反關係。

(3)R是對稱關係。

(4)R是反對稱關係。

(5)R是傳遞關係。

例2利用定理1判斷例1中各關係具有的性質。

解：5種性質都不具備，原因如下。

(1)，而，所以，故不具有自反性。

(2)，故不具有自反性。

(3) ，故不是對稱的。

(4)，故不是反對稱的。

(5) ，故不是傳遞的。

同理可以判斷：

是對稱的，不是自反的、反自反的、反對稱的、傳遞的；

是自反的、對稱的，不是反自反的、反對稱的、傳遞的；

是反自反的、反對稱的、傳遞的，不是自反的、對稱的；

是自反的、反對稱的、傳遞的，不是反自反的、對稱的；

是反自反的、反對稱的、傳遞的，不是自反的、對稱的。

相關概念

二元關係

設A，B是兩個集合，R是A×B的任意一個子集，即

則稱R為從集合A到集合B的一個二元關係，簡稱為從A到B的一個二元關係。

若 稱R為空關係。

若R=A×B，稱為全關係。

當A=B時，稱二元關係 為A上的二元關係。

當A=B時，記 稱之為A上的恆等關係。

自反關係與反自反關係

定義1令R是A上的二元關係，若對於A中的每個 都有 ，則稱R具有自反性(或稱R是自反關係)。

即R是A上的自反關係 。

定義2令R是A上的二元關係，若不存在A中的 ，使得 ，則稱R具有反自反性(或稱R是反自反關係)。

即R是A上的反自反關係 。

自反的關係亦稱“具有反身性的關係”。對於類K中一個確定的關係R來說，若類K中任意的個體和它自身都具有關係R，則稱關係R在類K中為自反的關係。若類K中沒有一個個體和它自己具有關係R，則稱關係R在類K中為反自反的關係。若類K中有的個體和它自己具有關係R，而有的個體和它自己不具有關係R，則稱關係R在類K中為非自反的關係。例如，設類K為實數域，則等於關係“=”是自反的關係，大於關係“>”，小於關係“<”都是反自反的關係。“x的平方數是Y”的這種關係就是非自反的關係。因為0的平方數是0，1的平方數是1，即當x為0(或1)時，y也同時為0(或1)，但當x為其它實數時，x的平方數y就不能再與x相同了。所以，“x的平方數是y”的這種關係就既不是自反的關係，也不是反自反的關係，而是非自反的關係。