設 R是 A上的一個二元關係,若對於 A中的每一個元素 a, (a,a)都屬於 R,則稱 R為自反關係。換言之,在自反關係中, A中每一個元素與其自身相關。
基本介紹
- 中文名:自反關係
- 外文名:reflexive relation
- 所屬學科:邏輯學、數學
- 屬性:二元關係的一種
- 相關概念:反自反關係、二元關係等
基礎知識
二元關係
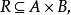



自反關係與反自反關係




例題解析
 圖1
圖1 圖2
圖2
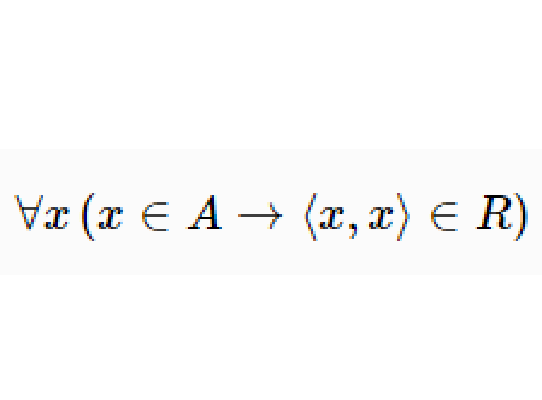
設 R是 A上的一個二元關係,若對於 A中的每一個元素 a, (a,a)都屬於 R,則稱 R為自反關係。換言之,在自反關係中, A中每一個元素與其自身相關。
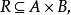







 圖1
圖1 圖2
圖2
(1)自反關係:自反關係是事物與其自身發生的某種關係。如:他自殺了。(2) 非自反關係:自身不能發生的關係。如:侵略、壓迫。關係主項數量 自反性關係有一個關係主項,是一項關係。對稱性關係有兩個關係主項,是兩項關係。傳遞性...
實際上D規定的就是兩個實數“相等”這個關係,即任何(x,y)屬於D意味著x=y。易驗證,此關係具自反性,因為(x,x)總屬於D。社會學中的自反性 維度一:社會學理論一般使用自反性概念是屬於認識範圍,以他們的定義:廣義的自反性...
關係邏輯的理論認為,由於事物之間存在著各種各樣的關係,因而,命題不只是可以表達主項與謂項的隸屬與非隸屬關係(“S是P”或“S不是P”)。而且,也可以表達其他一些關係,如同一關係、屬於關係、包含關係、自反關係、對稱關係、傳遞...
定義 集合A的一個關係R叫做一個非自反關係,假如R滿足:(1)非自反性: a∈A=>aRa;(2)對稱性: a,b∈A,aRb=>bRa;(3)傳遞性: a,b,c∈A,aRb,bRc=>aRc。設R是A上的關係。若對所有a∈A,均有(a,a)∈ R,...
vacuously)。非對稱關係亦即反對稱的非自反關係。()。一個n元素集上共有 個反對稱關係。自反的、對稱的且可遷的關係稱為等價關係,自反的且可遷的關係稱為擬序關係,自反的、可遷的且反對稱的關係稱為序關係。
令A={1,2,3}、R={,},求R的自反閉包。解:由於R缺少序偶,R不是自反關係,添加該序偶後則變成自反關係(即,在關係矩陣中,對角線上的數字均為1)。所以R的自反閉包r(R)={,,}。由求自反閉包的過程可以得到:r(R)=RUI ...
二元關係的數目 在一個有n個元素的集合(簡稱n元素集)上,一共有 個可能的二元關係。註:反自反關係和自反關係的數目一樣多。嚴格偏序(反自反的傳遞關係)的數目和偏序的一樣多。全序即是那些同時是全預序的偏序。透過容斥原理的...
《萬物理論:自反性的物質、生命、系統和宇宙》是一本2022年機械工業出版社出版的圖書,作者是麥可·J. 斯皮維(Michael J. Spivey)。內容簡介 許多人相信“自我”位於內心深處,一座“內在的聖殿”中存放著關於“自我”的所有重要假說...
定理1 設R是A上的二元關係,則 (1) R是自反關係 。(2) R是反自反關係 。(3)R是對稱關係 。(4)R是反對稱關係 。(5)R是傳遞關係 。例2利用定理1判斷例1中各關係具有的性質。解:5種性質都不具備,原因如下。(1),而 ...
自反性問題來自於不變子空間問題,對它的研究將揭示空間和運算元的關係;Lie結構和Jordan結構是運算元代數上兩種重要的非結合結構,對它們的研究將拓展運算元代數在量子力學等學科中的套用;而將函式空間上的Banach-Stone定理推廣到自反代數和半叉...
三角形的全等與相似關係,實數的大小比較關係、方程與不等式的同解關係、命題間的等價關係等.有的關係還具有若干基本性質.如數的相等關係、式的恆等關係具有自反性(即((b' a> (a=a;、對稱性(只要a=6,就有6=a)、傳遞性(只要a...
《自反性超越》是2010年6月1日華中師範大學出版社出版的圖書,作者是魏天真。本書主要講述了女性寫作的反女性主義症候,探討女性主義觀念下的女性文學寫作的問題與癥結等。內容簡介 本書的研究對象是20世紀90年代以來的中國女性小說,第二...
4.3.1 自反與反自反關係93 4.3.2 對稱與反對稱關係94 4.3.3 傳遞關係95 4.3.4 關係性質的等價描述與判定95 思考與練習4.397 4.4 關係的閉包98 4.4.1 閉包的概念98 4.4.2 閉包計算99 思考與...
2.4關係的圖形表示31 2.4.1實數R上的關係31 2.4.2集合上關係的有向圖32 2.4.3有限集上關係的圖示32 2.5關係的合成33 2.5.1關係合成33 2.5.2關係的合成與關係矩陣34 2.6關係的類型34 2.6.1自反關係34 2.6.2對稱...
第10章 關係中的算法 10.1 判斷關係R是否為自反關係及對稱關係 10.2 判斷關係R是否為可傳遞關係 10.3 判斷關係R是否為等價關係 10.4 求等價類 10.5 求極大相容類 10.6 關係的合成運算 10.7 關係的閉包運算(1)10.8 關係...
擬序(quasi-order)是一種特殊的二元關係,它是集合上具有反自反性及可傳遞性的二元關係。如a為一固定複數,對於任意複數x,y,有xR₁y若且唯若|x-a|≥|y-a|。又如對於有向圖G的任意兩個節點u,v,有uR₂v若且唯若u=...
