基本介紹
- 中文名：二元關係
- 外文名：Binary Relation
- 適用範圍：數理科學
定義,特殊的二元關係,性質,關係矩陣,關係圖,關係的運算,關係的閉包,二元關係的數目,
定義
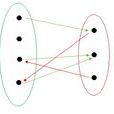
集合X與集合Y上的二元關係是R=(X,Y,G(R))，其中G(R)，稱為R的圖，是笛卡兒積X×Y的子集。若 (x,y) ∈G(R) ，則稱x是R-關係於y，並記作xRy或R(x,y)。否則稱x與y無關係R。但經常地我們把關係與其圖等同起來，即：若R⊆X×Y，則R是一個關係。
例如：有四件物件 {球，糖，車，槍} 及四個人 {甲，乙，丙，丁}。 若甲擁有球，乙擁有糖，及丁擁有車，即無人有槍及丙一無所有— 則二元關係"為...擁有"便是R=({球，糖，車，槍}, {甲，乙，丙，丁}, {(球,甲), (糖,乙), (車,丁)})。
其中 R 的首項是物件的集合，次項是人的集合，而末項是由有序對（物件，主人）組成的集合。比如有序對（球，甲）∈G(R)，所以我們可寫作"球R甲"，表示球為甲所擁有。
不同的關係可以有相同的圖。以下的關係 ({球，糖，車，槍}, {甲，乙，丁}, {(球,甲), (糖,乙), (車,丁)} 中人人皆是物主，所以與R不同，但兩者有相同的圖。話雖如此，我們很多時候索性把R定義為G(R)， 而 "有序對 (x,y) ∈G(R)" 亦即是 "(x,y) ∈R"。
若X=Y，則稱R為X上的關係。
特殊的二元關係
註：下文我們將採用把二元關係R定義為A × A的子集的做法。
設A是一個集合，則：
空集∅稱作A上的空關係（因為∅也是A × A的子集）。
EA = A × A稱作A上的全域關係。
IA = {(x,，x)： x∈A} 稱作A上的恆等關係。
性質
關係的性質主要有以下五種：自反性，反自反性，對稱性，反對稱性和傳遞性。
自反性：
。
在集合X上的關係R，如對任意
，有
，則稱R是自反的。
反自反性（自反性的否定的強形式）：
。
對稱性：
。
在集合X上的關係R，如果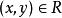有
則必有
，則稱R是對稱的。
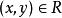
反對稱性（不是對稱性的否定）：
。
非對稱性（對稱性的否定的強形式）：
。
非對稱關係是滿足反自反性的反對稱關係。
傳遞性：
。
實例
例1：
設A={1,2,3},R1,R2和R3是A上的關係，其中：R1={<1,1>,<2,2>}；R2={<1,1>,<2,2>,<3,3>,<1,2>}；R3={<1,3>}，則R1不是自反的，R3是反自反的，R2是自反的但不是反自反的。
例2：
設A={1,2,3},R1,R2,R3和R4是A上的關係，其中：R1={<1,1>,<2,2>}；R2={<1,1>,<1,2>,<2,1>}；R3={<1,2>,<1,3>}；R4={<1,2>,<2,1>,<1,3>}，則R1既是對稱的也是反對稱的。R2是對稱的但不是反對稱的。R3是反對稱的但不是對稱的。R4既不是對稱的也不是反對稱的。
例3：
設A={1,2,3}，R1,R2和R3是A上的關係，其中：R1={<1,1>,<2,2>}；R2={<1,2>,<2,3>}；R3={<1,3>}，則R1和R3是A上的傳遞關係，R2不是A上的傳遞關係。
關係矩陣
設
及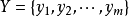
，R是X與Y上的二元關係，令
，則0,1矩陣
稱為R的關係矩陣，記作MR。
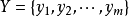
關係圖
設R集合A到B上的二元關係，令圖G=(V,E)，其中頂點集合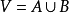
，邊集合為E ，且對於任意的
，規定
若且唯若
。則稱圖G是關係R的關係圖。
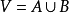
關係的運算
關係的基本運算有以下幾種：
設R為二元關係。
R中所有有序對的第二元素構成的集合稱為R的值域，記作ran(R) ，即
。
R的定義域和值域的並集稱作R的域，記作fld(R)，即
。
R的逆關係，簡稱R的逆，記作
，其中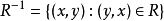
。
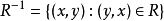
設S也是一個二元關係。R和S的合成記作
，其定義為
。
若R是一個集合A上的二元關係，可以在自然數範圍內定義R的n次冪。首先規定
，再遞歸定義
。可以證明有
，
成立。
與關係性質的聯繫
設R為集合A上的關係，下面給出的六種性質成立的充要條件：
R在A上自反若且唯若
；
R在A上反自反若且唯若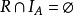
；
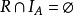
R在A上對稱若且唯若
；
R在A上反對稱若且唯若
；
R在A上非對稱若且唯若
；
R在A上傳遞若且唯若
。
關係的閉包
設R是非空集合A上的關係， R的自反（對稱或傳遞）閉包是A上的關係R' ，滿足：
(1) R'是自反的（對稱的或傳遞的）。
(2)
。
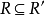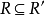
(3) 對A上任何包含R的自反（對稱或傳遞）關係R''有
。
下列給出了構造閉包的方法：
對於有限集合A 上的關係R ，存在一個正整數s，使得
，且s不超過A的元素數。
求傳遞閉包是圖論中一個非常重要的問題，例如給定了一個城市的交通地圖，可利用求傳遞閉包的方法獲知任意兩個地點之間是否有路相連通。可以直接利用關係矩陣相乘來求傳遞閉包，但那樣做複雜度比較高；好一點的辦法是在計算矩陣相乘的時候用分治法降低時間複雜度；但最好的方法是利用基於動態規劃的Floyd-Warshall算法來求傳遞閉包。
二元關係的數目
在一個有n個元素的集合（簡稱n元素集）上，一共有
個可能的二元關係。
在n元素集上各種二元關係的數目 | ||||||||
n | 所有 | 傳遞 | 自反 | 預序 | 偏序 | 全預序 | 全序 | 等價關係 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
2 | 16 | 13 | 4 | 4 | 3 | 3 | 2 | 2 |
3 | 512 | 171 | 64 | 29 | 19 | 13 | 6 | 5 |
4 | 65536 | 3994 | 4096 | 355 | 219 | 75 | 24 | 15 |
A002416 | A006905 | A053763 | A000798 | A001035 | A000670 | A000142 | A000110 | |
