算術

算術是數學中最古老、最基礎和最初等的部分，它研究數的性質及其運算。把數和數的性質、數和數之間的四則運算在套用過程中的經驗累積起來，並加以整理，就形成了最古老的一門數學——算術。在古代全部數學就叫做算術，現代的代數學、數論等最初就是由算術發展起來的。後來，算學、數學的概念出現了，它代替了算術的含義，包括了全部數學，算術就變成了其中的一個分支。

基本介紹

• 中文名：算術
• 外文名：arithmetic
• 研究對象：自然數和非負分數
• 研究內容：數的性質及其運算
• 相關書籍：《九章算術》、《算術》等
• 所屬學科：數學

基本介紹

算術（arithmetic）是數學的一個基礎分支。它以自然數和非負分數為主要對象。算術的內容包括兩部分，一部分討論自然數的讀法、寫法和它的基本運算，這一部分包括進位制和記數法，主要是十進位制，其他的進位制與十進位制僅是採用的基數不同，都可以仿照十進位數的原理和原則進行計算，算術的另一部分包括算術運算的方法與原理的套用。如分數與百分數計算，各種量及其計算，比和比例，以及算術套用題。

算術

自然數或正整數的數學理論就是眾所周知的算術。至於幾何、 代數等許多數學分支學科的名稱，都是後來很晚的時候才有的。

國外系統地整理前人數學知識的書，要算是希臘的歐幾里得的《幾何原本》最早。《幾何原本》全書共十五卷，後兩卷是後人增補的。全書大部分是屬於幾何知識，在第七、八、九卷中專門討論了數的性質和運算，屬於算術的內容。

拉丁文的“算術”這個詞是由希臘文的“數和數（音屬）數的技術”變化而來的。“算”字在中國的古意也是“數”的意思，表示計算用的竹籌。中國古代的複雜數字計算都要用算籌。所以“算術”包含當時的全部數學知識與計算技能，流傳下來的最古老的《九章算術》以及失傳的許商《算術》和杜忠《算術》，就是討論各種實際的數學問題的求解方法。

古代算術工具

算術規律

算術的基礎在於：整數的加法和乘法服從某些規律。為了要敘述這些具有普遍性的規律，不能用像1，2，3這種表示特定數的符號。兩個整數，不管它們的次序如何，它們的和相同。例如1+2=2+1。

算術不只是簡單的計算

這一命題僅僅是這一般規律的一個特殊例子。因此當我們希望表示整數之間的某個關係——不論涉及的一些特定的整數值如何——是正確的，可以用字母a，b，c，…作為表示整數的符號。於是，我們所熟知的五個算術規律可敘述為：

前兩個是加法和乘法的交換律，它說明人們可以交換加法或乘法中元素的次序。第三個是加法的結合律，它表明三個數相加時，或者我們把第一個加上第二個與第三個的和；或者我們把第三個加上第一個與第二個的和，其結果都相同。第四個是乘法的結合律。最後一個是分配律，它表明用一個整數去乘一個和時，我們可以用這整數去乘這和的每一項，然後把這些乘積加起來。

算術演變

算術是數學的一個分支，其內容包括自然數和在各種運算下產生的性質，運算法則以及在實際中的套用。可是，在數學發展的歷史中算術的含義要廣泛得多。

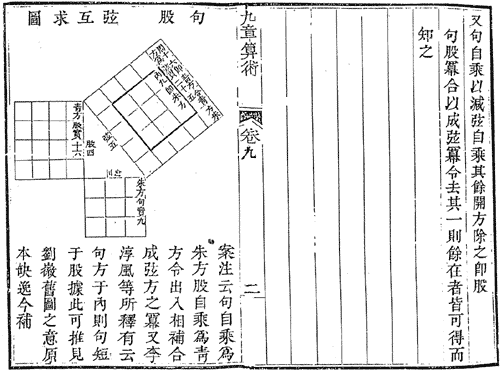九章算術中的勾股定理

在中國古代，算是一種竹製的計算器具，算術是指操作這種計算器具的技術，也泛指當時一切與計算有關的數學知識。算術一詞正式出現於《九章算術》中。《九章算術》分為九章，即方田、粟米等，大都是實用的名稱。如“方田”是指土地的形狀，講土地面積的計算，屬於幾何的範圍；“粟米”是糧食的代稱，講的是各種糧食間的兌換，主要涉及的是比例，屬於算術的範圍。可見，當時的“算術”是泛指數學的全體，與現代的意義不同。

直到宋元時代，才出現了“數學”這一名詞，在數學家的菱中，往往數學與算學並用。當然，此處的數學僅泛指中國古代的數學，它與古希臘數學體系不同，它側重研究算法。

從19世紀起，西方的一些數學學科，包括代數、三角等相繼傳入中國。西方傳教士多使用數學，日本後來也使用數學一詞，中國古算術則仍沿用“算學”。1953年，中國數學會成立數學名詞審查委員會，確立起“算術”的意義，而算學與數學仍並存使用。1937年，清華大學仍設“算學系”。1939年為了統一起見，才確定專用“數學”。

產生髮展

關於算數的產生，還是要從數談起。數是用來表達、討論數量問題的，有 不同類型的量，也就隨著產生了各種不同類型的數。遠在古代發展的最初階段，由於人類日常生活與生產實踐中的需要，在文化發展的最初階段就產生了最簡單的自然數的概念。

算術來源於對量的認識

自然數的一個特點就是由不可分割的個體組成。比如說樹和羊這兩種事物，如果說兩棵樹，就是一棵再一顆；如果有三隻羊，就是一隻、一隻又一隻。但不能說有半棵樹或者半隻羊，半棵樹或者半隻羊充其量只能算是木材或者是羊肉，而不能算作樹和羊。

數和數之間有不同的關係，為了計算這些數，就產生了加、減、乘、除的方法，這四種方法就是四則運算。

把數和數的性質、數和數之間的四則運算在套用過程中的經驗累積起來，並加以整理，就形成了最古老的一門數學——算術。

在算術的發展過程中，由於實踐和理論上的要求，提出了許多新問題，在解決這些新問題的過程中，古算術從兩個方面得到了進一步的發展。

一方面在研究自然數四則運算中，發現只有除法比較複雜，有的能除盡，有的除不盡，有的數可以分解，有的數不能分解，有些數又大於1的公約數，有些數沒有大於1的公約數。為了尋求這些數的規律，從而發展成為專門研究數的性質、脫離了古算術而獨立的一個數學分支，叫做整數論，或叫做初等數論，並在以後又有新的發展。

另一方面，在古算術中討論各種類型的套用問題，以及對這些問題的各種解法。在長 期的研究中，很自然地就會啟發人們尋求解這些套用問題的一般方法。也就是說，能不能找到一般的更為普遍適用的方法來解決同樣類型的套用問題，於是發明了抽象的數學符號，從而發展成為數學的另一個古老的分支，指就是初等代數。

算術

數學如此發展，算術已不再是數學的一個分支，我們通常提到的算術，只是作為國小里的一個教學科目，目的是使學生理解和掌握有關數量關係和空間形式的最基礎的知識，能夠正確、迅速地進行整數、小數、分數的四則運算，初步了解現代數學中的一些最簡單的思想，具有初步的邏輯思維能力和空間觀念。

區別比較

現代國小數學的具體內容，基本上還是古代算術的知識，也就是說，古代算術和現代算術的許多內容上是相同的。不過現代算術和古代算術也還存在著區別。

德國數學家高斯

首先，算術的內容是古代的成人包括數學家所研究的對象，這些內容已變成了少年兒童的數學。其次，在現代國小數學裡，總結了長期以來所歸結出來的基本運算性質，即加法、乘法的交換律和結合律，以及乘法對加法的分配律。這五條基本運算定律，不僅是國小數學裡所學習的數運算的重要性質，也是整個數學裡，特別是代數學里著重研究的主要性質。

第三，在現代的國小數學裡，還孕育著近代數學裡的集合和函式等數學基礎概念的思想。比如，和、差、積、商的變化，數和數之間的對應關係，以及比和比例等。

另外，國小數學裡，還包含有十六世紀才出現的十進小數和它們的四則運算。應當提出的是十進小數不是一種新的數，而可以被看作是一種分母是10的方冪的分數的另一種寫法。

現代的代數學、數論等最初就是由算術發展起來的。後來，算學、數學的概念出現了，它代替了算術的含義，包括了全部數學，算術就變成了一個分支了。因此，也可以說算術是最古老的分支。

相關書籍

《算術》（Arithmetica）是古希臘後期數學家丟番圖的一部名著，著作原有13卷，長期以來，大家都以為只有1464年在威尼斯發現的前6卷希臘文抄本，後在馬什哈德（伊朗東北部）又發現4卷阿拉伯文譯本。

法國數學家費馬

《算術》事實上是一部代數著作，其中包含有一元或多元一次方程的問題，二次不定方程問題以及數論方面的問題，現存6卷中共有189題，幾乎一題一法，各不相同。雖然後人將其歸成五十多個類，但是仍無一般的方法可尋。並且，著作中引用了許多縮寫符號，如未知量及其各次冪用S、△r、Kr、△r△、△Kr、KrK等符號。無論從內容與形式上講，這種完全脫離幾何的特徵，與當時古希臘歐幾里得幾何盛行的時尚大異其趣。因此，丟番圖的《算術》雖然代表了古希臘代數學的最高水平，但是它遠遠超出了同時代人，而不為同時代人所接受，很快就被湮沒，沒有對當時數學的發展產生太大的影響。

直到15世紀《算術》被重新發掘，鼓舞了一大批數學家在此基礎之上，把代數學大大向前推進了。首先是法國數學家蓬貝利認識到《算術》的重大價值，他的同胞韋達正是在丟番圖縮寫代數的啟示下才做出了符號代數的貢獻，到17世紀，費馬手持一本《算術》，並在其空白處寫寫畫畫，竟把數論引上了近代的軌道。《算術》中的不定分析，對現代數學影響也很深遠，在不同數域上，凡是涉及不定方程求解問題，都稱之為“丟番圖方程”或“丟番圖分析”。

算術使用

十進制

在基數（前十個非負整數0，1，2，……，9）的基礎上構建所有實數。一個十進制數由一個基數序列組成，每一位數字的命名取決於其相對於小數點的位置。例如：507.36表示5個100（10），加0個10（10），加7個最小整數單位1（10），加3個0.1（10），加6個0.01（10）。該計數法的一個要點（也是其實現的難點）是對0與其它基數一視同仁。

算術運算

算術運算指加法、減法、乘法和除法,但有時也包括較高級的運算(例如百分比、平方根、取冪和對數)。算術按運算次序進行，無何集合可以進行加減乘除四則運算（除以零除外），而四則運算合乎基本公理，都可稱之為一個域（Field）。

加法

主條目：加法

加法是基本算術運算。簡單來說，加法將兩個數字結合，成為一個數字，稱之為“和”。把多於兩個數相加，可以視為重複的加法；這個過程稱為求和，包括在級數中把無窮多個數相加。1的重複加法是計數的最基本的形式。

加法滿足交換律和結合律。加法的單位元是0，也就是說，把任何數加上0都得到相同的數。另外，加法的逆元素就是相反數，也就是說，把任何數加上它的相反數都得出單位元0。例如，7的相反數是(-7)，所以7 + (-7) = 0。

減法

主條目：減法

減法是加法的相反。減法是求出兩個數（被減數和減數）的差。如果被減數大於減數，那么差為正數；如果被減數小於減數，那么差為負數；如果它們相等，那么差為0。

減法既不滿足交換律又不滿足結合律。由於這個原因，把減法視為被減數和減數的相反數的加法通常是很有幫助的，也就是說，a−b=a+ (−b)。當寫成加法時，所有加法的性質都成立。

乘法

主條目：乘法

乘法本質上是一組相同數字的重複累加或總和。乘法運算可得出乘數與被乘數（有時被通稱為因數）的乘積。

乘法運算（由於其本質是重複累加）具有交換性和結合性；進而，它對加法和減法運算具有分配性。乘法單位為1，即，用1乘以任意數的結果仍為該數。並且，任意數字的乘法逆元素是其倒數，即，用一個數的倒數乘以該數，其結果為乘法單位：1。

除法

主條目：除法

除法是乘法的逆運算。除法運算得到兩個數的商：被除數除以除數。任何被除數被零除是沒有定義的。對於正數，如果被除數大於除數，其商大於1，否則商小於1（對於負數和-1有類似的規則）。商乘以除數其結果總是被除數。

除法運算不具有交換性和結合性。正如可以將減法視為加法，除法亦可被視作被除數和除數的倒數之間的乘法運算，即，a÷b=a× /b。當被寫為乘積形式，運算遵循乘法的所有特性。

算術教育

近現代的初等數學教育，可以說是在晚清(1903)頒布癸卯學制,廢除科舉,興辦國小、中學後才開始的。當時國小設算術課，中學設數學課（包括算術、代數、幾何、三角、簿記）。民國初年(1912～1913)公布壬子癸丑學制，中學由五年改為四年，數學課程不再講授簿記。執行時間最久的是1922年公布的壬戌學制，將國小、中學都改為六年，各分初高兩級，初小四年,高小二年,初高中皆三年。國中數學講授算術、代數、平面幾何，高中數學講授平面三角、高中幾何、高中代數、平面解析幾何（高中曾分文理兩科，部分理科加授立體解析幾何和微積分初步），這個學制基本沿用到1949年。中華人民共和國成立後，中國小的教育進行了改革，學制大都改為國小六年,初高中各三年,國中逐步取消算術課。50年代高中數學一度停授平面解析幾何，後又恢復並增授微積分初步以及機率論和電子計算機的初步知識。