基本介紹
- 中文名:逆元素
- 外文名:Inverse element
- 學科:數學
- 作用:取消另一給定元素運算的元素
- 集合:二元運算
基本概念


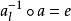





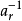

例題解析

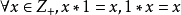

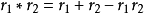


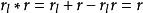

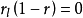

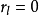


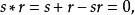

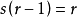
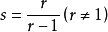

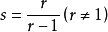
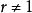

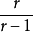


左右逆元素相等且唯一的條件




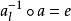





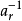


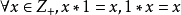

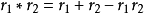


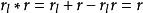

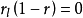

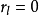


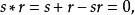

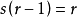
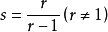

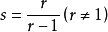
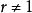

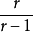



逆元素是指一個可以取消另一給定元素運算的元素,在數學裡,逆元素廣義化了加法中的加法逆元和乘法中的倒數。...
乘法逆元,是指數學領域群G中任意一個元素a,都在G中有唯一的逆元a‘,具有性質a×a'=a'×a=e,其中e為該群的單位元。...
擬逆元是巴拿赫代數中的一個概念。擬逆元包括左擬逆元和右擬逆元。...... 擬逆元是巴拿赫代數中的一個概念。擬逆元包括左擬逆元和右擬逆元。...
若R的每個非零元素都有逆元素,則R稱為一個體或可除環。四元數代數就是典型的體。在體的定義中再規定其乘法適合交換律,就是域的定義。...
在數學中,群表示一個擁有滿足封閉性、滿足結合律、有單位元、有逆元的二元運算的代數結構,包括阿貝爾群、同態和共軛類。...
在抽象代數中,除環(也稱為斜體)是一個非零環,其中每個非零元素a都具有乘法逆,即具有x·a=a·x的元素x。換句話說,一個環若且唯若單位組等於所有非零元素...
除環(division ring),又譯反稱域(skew field)、體,是如下定義的一個環: 至少有一個非零元素,這些非零元素稱為單位(Unit) 非零元素都存在逆元素(左逆元素...
向量加法的單位元:V 里有一個叫做零向量的 0,∀ v ∈ V , v + 0 = v; 向量加法的逆元素:∀v∈V, ∃w∈V,使得 v + w = 0; 標量乘法分...
(3)單位元素:置換群的單位元素本身就是偶置換;(4)逆元素:(i k)的逆元素為(i k),p = (i1 j1) (i2 j2) ... (ik jk)的逆元素為p-1 = (ik ...
穩定子群亦稱穩定化子。一種特殊的子群。設群G作用在集合X上,x∈X,G中作用在x上使x不變的元素的全體,即{g∈G|xg=x},它是G的一個子群,稱為x的穩定...
設G是1,2,...,n 的置換群。若k是1…n中的某個元素,G中使k保持不變的置換的全體,記以Zk,叫做G中使k保持不動的置換類,簡稱k不動置換類。...
子群的單位元亦是群的單位元:若G是個有單位元素eG的群,且H為具有單位元素eH之G的子群,則eH = eG。一個子群內的一元素之逆元素為群內的此元素的逆元素:...
商模(quotient module)是模論的重要概念之一,模M與它的商模M-之間的性質有著密切的聯繫。它是將A模M的元素進行陪集分類後所得到的新模,亦稱“差模”。設是...
一般說來,群指的是滿足以下四個條件的一組元素的集合:(1)封閉性 (2)結合律成立 (3)單位元存在 (4)逆元存在。...
如果群中的運算被稱為“加法”,那么同樣的概念稱為“加法逆”。乘法逆的具體定義可以參見群的逆元素概念。差倒數舉例 比如說:1/5×5=1,則1/5和5就互為倒數...
若有整數a′能滿足同餘式a′a≡1(mod m),則稱a′是a(mod m)的數論倒數,或逆元。例如,設整數a=2,m=3,且(2,3)=1,當a′=2時,有a′a≡2·2≡4...
播音主持畢業的郭春雨,他身上布滿叛逆元素,視覺系妝容、四核搖滾、地下說唱,這些在全世界音樂圈裡都算得上先鋒的元素,在這個年輕人身上都被一一的展現。...
在環中,所有可逆元素叫環的單位,所有單位對乘法可構成一個乘法群,叫環的單位群。...... 在環中,所有可逆元素叫環的單位,所有單位對乘法可構成一個乘法群,叫...
設R有單位元e,y是x的擬逆元,則e-y就是e-x的逆元。可逆元稱為正則的,非可逆元稱為奇異的。...
