最低公倍數

兩個或多個整數公有的倍數叫做它們的公倍數，其中除0以外最小的一個公倍數就叫做這幾個整數的最低公倍數。整數a，b的最低公倍數記為[a，b]，同樣的，a，b，c的最低公倍數記為[a，b，c]，多個整數的最低公倍數也有同樣的記號。

與最低公倍數相對應的概念是最大公約數，a，b的最大公約數記為（a，b）。關於最低公倍數與最大公約數，我們有這樣的定理：(a,b)x[a,b]=ab(a,b均為整數)。

基本介紹

• 中文名：最低公倍數
• 外文名：Least Common Multiple
• 定義：幾個數的最小公倍數
• 算法：藉助最大公約數來計算
• 對象：兩個及兩個以上的數
• 領域：數學

定義

幾個數共有的倍數叫做這幾個數的公倍數，其中除0以外最小的一個公倍數，叫做這幾個數的最低公倍數。

自然數a、b的最低公倍數可以記作[a,b],自然數a、b的最大公因數可以記作(a、b)，當(a、b)=1時,[a、b]= a×b。如果兩個數是倍數關係，則它們的最低公倍數就是較大的數，相鄰的兩個自然數的最低公倍數是它們的乘積。最低公倍數=兩數的乘積/最大公約（因）數, 解題時要避免和最大公約（因）數問題混淆。

最低公倍數的適用範圍：分數的加減法，中國剩餘定理(正確的題在最低公倍數內有解，有唯一的解)。因為，素數是不能被1和自身數以外的其它數整除的數；素數X的N次方，是只能被X的N及以下次方，1和自身數整除。所以，給最低公倍數下一個定義：S個數的最低公倍數，為這S個數中所含素因子的最高次方之間的乘積。

例如：1，求756，4400，19845，9000的最低公倍數？

因756=2*2*3*3*3*7，4400=2*2*2*2*5*5*11，19845=3*3*3*3*5*7*7，9000=2*2*2*3*3*5*5*5，這裡有素數2，3，5，7，11．2最高為4次方16，3最高為4次方81，5最高為3次方125，7最高為2次方49，還有素數11。得最低公倍數為16*81*125*49*11=87318000．2，自然數1至50的最低公倍數，因為，√50≈7，所以，在50之內的數只有≤7的素數涉及N次方。在50之內，2的最高次方的數為32，3的最高次方的數為27，5的最高次方的數為25，7的最高次方的數為49，其餘為50之內的素數。所以，1，2，3，4，5，6，…，50的最低公倍數為：32*27*25*49*11*13*17*19*23*29*31*37*41*43*47=3099044504245996706400

性質及特點

最低公倍數的性質：公倍數(common multiple)指在兩個或兩個以上的自然數中，如果它們有相同的倍數，這些倍數就是它們的公倍數，其中除0以外最小的一個公倍數，叫做這幾個數的最低公倍數。

最大公因數和最低公倍數之間的性質：兩個自然數的乘積等於這兩個自然數的最大公約數和最低公倍數的乘積。最低公倍數的計算要把三個數的公有質因數和獨有質因數都要找全，最後除到兩兩互質為止。

最低公倍數特點：倍數的只有最小的沒有最大，因為兩個數的倍數可以無窮大。

最低公倍數計算方法：

1、分解質因數法

2、公式法。

適用範圍

分數的加減法，中國剩餘定理(正確的題在最低公倍數內有解，有唯一的解)．

將最低公倍數套用到實際中，稱之為最低公倍數法。最低公倍數法是統計學的一個術語，以各備選方案計算期的最低公倍數作為比選方案的共同計算期，並假設各個方案均在這樣一個共同的計算期內重複進行。

計算方法

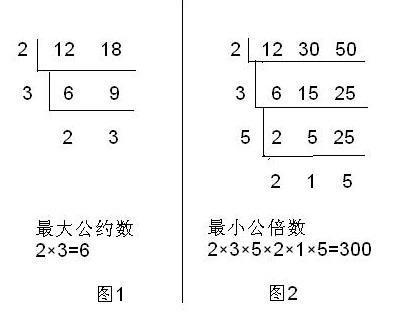
分解質因數法

先把這幾個數的質因數寫出來，最低公倍數等於它們所有的質因數的乘積（如果有幾個質因數相同，則比較兩數中哪個數有該質因數的個數較多，乘較多的次數）。

比如求45和30的最低公倍數。
45=3*3*5
30=2*3*5
不同的質因數是2。5，3是他們兩者都有的質因數，由於45有兩個3，30隻有一個3，所以計算最低公倍數的時候乘兩個3.
最低公倍數等於2*3*3*5=90
又如計算36和270的最低公倍數
36=2*2*3*3
270=2*3*3*3*5
不同的質因數是5。2這個質因數在36中比較多，為兩個，所以乘兩次；3這個質因數在270個比較多，為三個，所以乘三次。
最低公倍數等於2*2*3*3*3*5=540
20和40的最低公倍數是40

最大公約數，最低公倍數

公式法

由於兩個數的乘積等於這兩個數的最大公約數與最低公倍數的積。即（a，b）×[a，b]=a×b。所以，求兩個數的最低公倍數，就可以先求出它們的最大公約數，然後用上述公式求出它們的最低公倍數。

例如，求[18，20]，即得[18，20]=18×20÷（18，20）=18×20÷2=180。求幾個自然數的最低公倍數，可以先求出其中兩個數的最低公倍數，再求這個最低公倍數與第三個數的最低公倍數，依次求下去，直到最後一個為止。最後所得的那個最低公倍數，就是所求的幾個數的最低公倍數。

示例

例題1

兩個數的最大公因數是15,最低公倍數是90,求這兩個數分別是多少？

15×1=15,15×6=90；當a1b1分別是1和6是，a、b分別為15×1=15,15×6=90；當a2b2分別是2和3時,a、b分別為15×2=30,15×3=45。所以，這兩個數是15和90或者30和45。

例題2

兩個自然數的積是360,最低公倍數是120,這兩個數各是多少？

分析我們把這兩個自然數稱為甲數和乙數。因為甲、乙兩數的積一定等於甲、乙兩數的最大公因數與最低公倍數的積。根據這一規律，我們可以求出這兩個數的最大公因數是360÷120=3。又因為（甲÷3=a,乙÷3=b)中,3×a×b=120,a和b一定是互質數，所以,a和b可以是1和40,也可以是5和8。當a和b是1和40時，所求的數是3×1=3和3×40=120；當a和b是5和8時，所求的數是3×5=15和3×8=24。

例題3

甲、乙、丙三人是朋友，他們每隔不同天數到圖書館去一次。甲3天去一次，乙4天去一次，丙5天去一次。有一天，他們三人恰好在圖書館相會，問至少再過多少天他們三人又在圖書館相會？

分析從第一次三人在圖書館相會到下一次再次相會，相隔的天數應該是3、4、5的最低公倍數。因為3、4、5的最低公倍數是60,所以至少再過60天他們三人又在圖書館相會。

例題4

一塊磚長20厘米，寬12厘米，厚6厘米。要堆成正方體至少需要這樣的磚頭多少塊？

分析把若干個長方體疊成正方體，它的棱長應是長方體長、寬、高的公倍數。現在要求長方體磚塊最少，它的棱長應是長方體長、寬、高的最低公倍數，求出正方體棱長後，再根據正方體與長方體體積之間的關係就能求出長方體磚的塊數。

例題5

甲每秒跑3米，乙每秒跑4米，丙每秒跑2米，三人沿600米的環形跑道從同一地點同時同方向跑步，經過多少時間三人又同時從出發點出發？

分析甲跑一圈需要600÷3=200秒，乙跑一圈需要600÷4=150秒，丙跑一圈需要600÷2=300秒。要使三人再次從出發點一齊出發，經過的時間一定是200、150和300的最低公倍數。200、150和300的最低公倍數是600,所以，經過600秒後三人又同時從出發點出發。

套用實例

亡故的先父留下遺囑，

共有遺產17個元寶，

老大得元寶的二分之一、 17/2=8.5

老二得元寶的三分之一、 17/3=5.66666

老三得元寶的九分之一、 17/9=1.8

問他們每一個人分別應該分幾個元寶？

在《一代大商孟洛川》中是這樣做的

孟洛川拿來一個元寶加上去

好了，開始分元寶

答案是：老大9個元寶、老二6個元寶、老三2個元寶。

很不可思議吧？

很簡單的國中數學題老大分1/2,老二分1/3,老三分1/9

這三個數的最低公倍數就是18,即9/18+6/18+2/18=17/18,就是說他們老爺子給的這個比例和根本就沒到1,。即1-17/18=1/18,也就是說，直接分，那是分不完17元寶的。這樣這要用18這個最低公倍數就能分開，最後還剩一個。

編程實現

CoffeeScript

gcd = (a, b) -> # 最大公約數  return gcd b, a if a < b  # a,b中如果有一是0,回答另一  if b is 0 then a else gcd a % b scm = (a,b)->  # 求最低公倍數  a * b / gcd(a, b)

C#

public static float minGongBeiShu(intn1,intn2){int temp=Math.Max(n1,n2);n2=Math.Min(n1,n2);//n2中存放兩個數中最小的n1=temp;//n1中存放兩個數中最大的int product=n1*n2;//求兩個數的乘積while(n2!=0){n1=n1>n2?n1:n2;//使n1中的數大於n2中的數int m=n1%n2;n1=n2;n2=m;}return(product/n1);//最低公倍數}

C

#include<stdio.h>int gcd(int a,int b);int lcm(int a,int b);int main(void){int m,n,result_gcd,result_lcm;printf("求兩個數的最大公約數及最低公倍數？\n請輸入你想計算的兩個數：\n");scanf("%d%d",&m,&n);result_gcd=gcd(m,n);result_lcm=lcm(m,n);printf("最大公約數為：%d\n最低公倍數為：%d\n",result_gcd,result_lcm);return 0;}int gcd(int a,int b){int temp;if(a<b){//交換兩個數，使大數放在a上temp=a;a=b;b=temp;}while(b!=0){//利用輾除法，直到b為0為止temp=a%b;a=b;b=temp;}return a;}int lcm(int a,int b){int temp_lcm;temp_lcm=a*b/gcd(a,b);//最低公倍數等於兩數之積除以其最大公約數return temp_lcm;}

C++

#include<iostream>using namespace std;int GCD(int a,int b);int LCM(int a,int b);int main(){int num1,num2,gcd,lcm;cout<<"求兩個數的最大公約數及最低公倍數"<<endl<<endl;cout<<"請輸入兩個數：";cin>>num1>>num2;gcd=GCD(num1,num2);lcm=LCM(num1,num2);//輸出最大公約數和最低公倍數cout<<"最大公約數為："<<gcd<<endl;cout<<"最低公倍數為："<<lcm<<endl;system("pause");return 0;}int GCD(int num1,int num2){if(num1%num2==0)return num2;else return  GCD(num2,num1%num2);}int LCM(int a,int b){int temp_lcm;temp_lcm=a*b/GCD(a,b);//最低公倍數等於兩數之積除以最大公約數return temp_lcm;}

Fortran

!gcd()gets the greatest common divisor(i.e.,higest common factor)!lcm()gets the least common multipleprogram gcd_lcminteger::m,nwrite(*,*)'Please input two integers:'read(*,*)m,nwrite(*,*)'They have the greatest common divisor:',gcd(m,n)write(*,*)'They have the least common multiple:',lcm(m,n)containsinteger function lcm(mm,nn)integer,intent(in)::mm,nnlcm=mm*nn/gcd(mm,nn)end function lcm!BLinteger function gcd(mm,nn)integer,intent(in)::mm,nninteger::m,n,r,tm=mmn=nnif(m<n)thent=mm=nn=tendifdo while(r/=0)r=mod(m,n)if(r==0) exitm=nn=rend dogcd=nend function gcdend program gcd_lcm

PASCAL

//1、var a,b,ans:integer;function gcd(a,b:integer):longint;beginif b=0 then gcd:=aelse gcd:=gcd(b,a mod b);end;//2、var a,b,ans:integer;function gcd(a,b:integer):longint;beginreadln(a,b);ans:=(a*b) div gcd(a,b);gcd:=ans;end.

JAVA

Scanner in=new Scanner(System.in);　int a=in.nextInt();　int b=in.nextInt();　int c=a*b;　if(a<b){　int r=0;　r=a;a=b;b=r;　}　while(true){　int r=a%b;　if(r==0){　System.out.println("最低公倍數："+c/b);　break;　}else{　a=b;　b=r;　}}

Python

def gcd(n1,n2):    """greatest common divisor function """    return gcd(n2, n1 % n2) if n2 > 0 else n1def lcm(n1,n2):    """lowest common multiple function"""    return n1 * n2 // gcd(n1, n2)