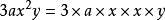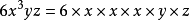公因式

公因式（common factor），即多項式各項都含有的相同因式。

基本介紹

• 中文名：公因式
• 外文名：common factor
• 拼音：gōng yīn shì
• 含義：多項式各項都含有的公共的因式
• 方法：提公因式法
• 學科：數學

基本內容

一個多項式中每一項都含有的相同的因式，叫做這個多項式各項的公因式。

如果一個多項式的各項含有公因式，那么可以把公因式提取出來進行因式分解，這種因式分解的方法叫做提取公因式法。

把一個多項式化成了幾個整式的積的形式，像這樣的式子變形叫做把這個多項式因式分解，也叫做把這個多項式分解因式。

公因式的確定方法：提取的公因式的是各項係數的最大公約數與各項都含有的相同字母的最低次數冪的積。

公因式

一般步驟

提取公因式法的一般步驟：

（1）確定應提取的公因式；

（2）多項式除以公因式，所得的商作為另一個因式；

（3）把多項式寫成這兩個因式的積的形式。

比較

公因式與最簡公分母二者在概念不同是有很大的區別，公因式是指多項式中各項都含有的因式，最簡公分母是各分母所有因式的最高次冪的積。

相同點：就“公”字而言，都是指的公共的。從確定方法來說，都要確定係數和相同字母。

不同點：對於最簡公分母，首先確定係數，係數是各分母係數最低公倍數；第二確定字母，相同字母取最高次冪，而對於只在一個分母中出現的字母，連同指數作為最簡公分母的一個因式。其次，正負性不同，一般情況下，公因式可正可負，最簡公分母通常取正。二者相同點和不同點歸納如下表。

	相 同 點	不 同 點
公 因 式	確定係數和字母	係數取最大公約數; 字母取最低次冪; 不同字母不取
最簡公分母		係數取最低公倍數; 字母取最高次冪; 不同字母要取

注意事項

1. 提公因式後，另一個因式：①項數應與原多項式的項數一樣；②不再含有公因式。
2. 公因式可以是數字、字母，也可以是單項式，還可以是多項式。
3. 多項式的第一項是係數為負數的項，一般地，應提出負係數的公因式。但應注意，這時留在括弧內的每一項的符號都要改變。

例題

例1.把2ac(b+2c)- (b+2c)分解因式。

解：2ac(b+2c) －(b+2c)
= (b+2c)(2ac-1)

例2.多項式有公因式嗎？是什麼？

解：，。

所以該多項式有公因式，應提取的公因式為。