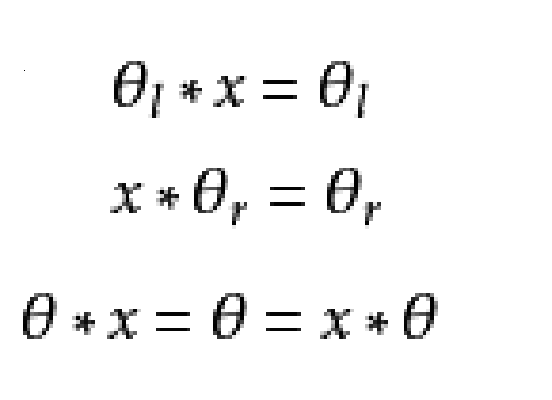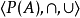設*是定義在集合S上的一個二元運算,如果有一個元θl∈S,使得對於任意的元素x∈A都有θl*x=θl,則稱θl為S中關於運算*的左零元;如果有一元素θr∈S,對於任意的元素x∈S都有x*θr=θr,則稱θr為S中關於運算*的右零元;如果S中有一元素θ,它既是左零元又是右零元,則稱θ為S中關於運算*的零元。
基本介紹
- 中文名:零元
- 外文名:zero element
- 所屬學科:離散數學
- 相關概念:左零元、右零元、二元運算等
定義



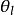











相關性質






例題解析




 | 1 | 2 | 3 | 4 |
1 | 1 | 2 | 4 | 1 |
2 | 1 | 2 | 3 | 4 |
3 | 1 | 2 | 3 | 4 |
4 | 1 | 2 | 3 | 4 |
△ | 1 | 2 | 3 | 4 |
1 | 2 | 2 | 1 | 4 |
2 | 2 | 2 | 2 | 2 |
3 | 1 | 2 | 3 | 4 |
4 | 1 | 2 | 4 | 3 |