基本介紹
- 中文名:丟番圖方程
- 外文名:Diophantine Equation
- 又名:不定方程、整係數多項式方程
- 分類:數學
- 提出:丟番圖
- 國家:希臘
定義
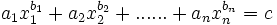 丟番圖方程
丟番圖方程
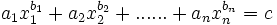 丟番圖方程
丟番圖方程丟番圖方程(Diophantine Equation):有一個或者幾個變數的整係數方程,它們的求解僅僅在整數範圍內進行。最後這個限制使得丟番圖方程求解與實數範圍方程求解有根本的不...
丟番圖(Diophantus)是古希臘亞歷山大學後期的重要學者和數學家(約公元246—330年,據推斷和計算而知)丟番圖是代數學的創始人之一,對算術理論有深入研究,他完全...
《廣義費馬方程與指數丟番圖方程》是2011年遼寧科學技術出版社出版的一本圖書,作者是佟瑞洲。...
《Gel'fond-Baker方法在丟番圖方程中的套用》系統地論述了Gel'fond-Baker方法在Thue方程、Thue-Mahler方程、廣義Ramanujan-Nagell方程、橢圓方程、超橢圓方程以及有理...
未知數個數多於方程個數,並且對解有一定限制(比如要求解為正整數等)的方程。數論中最古老的分支之一。古希臘的丟番圖早在公元3世紀就開始研究不定方程,因此常...
這相當於求解一次不定方程(indefinite equation)或一次丟番圖方程(Diophantine equation) ,其中,a,b,n為已知整數,求整數解x,y。這一方程有解的充要條件為(a,n...
能求出一個整係數方程的整數根,稱為丟番圖方程可解。希爾伯特問,能否用一種由有限步構成的一般算法判斷一個丟番圖方程的可解性?1970年,蘇聯的IO.B.馬季亞謝...
例如我們將於2002年舉辦有關於解析數論(Analytic Number Theory) 與丟番圖方程(Diophantine Equations) 的研討會。我們通常邀請一兩位專家策劃這樣的活動。...
數論是純粹數學的分支之一,主要研究整數的性質。整數可以是方程式的解(丟番圖方程)。有些解析函式(像黎曼ζ函式)中包括了一些整數、質數的性質,透過這些函式也可以...
他使用了kuṭṭaka (कुट्टक) 方法去解決丟番圖方程的一級問題。在代數方面,阿耶波多給出了有關整數的平方和立方求和的公式:...
希爾伯特的第十個問題,就是不定方程(又稱為丟番圖方程)的可解答性。這是希爾伯特於1900年在巴黎的國際數學家大會演說中,所提出的23個重要數學問題的第十題。...
裴蜀定理說明了對任何整數 a、b和它們的最大公約數 d ,關於未知數 x 和 y 的線性丟番圖方程(稱為裴蜀等式)。中文名 裴蜀定理 外文名 Bézout's identity...
希爾伯特問,能否用一種由有限步構成的一般算法判斷一個丟番圖方程的可解性?1970年,蘇聯的IO.B.馬季亞謝維奇證明了希爾伯特所期望的算法不存在。...
10.丟番圖方程可解性的判別;1970年,ю.Β.馬季亞謝維奇證明了希爾伯特所期望的一般算法不存在。11.係數為任意代數數的二次型問題;係數為任意代數數的二次型H....
斐波那契其他數學著作還有《平方數書》(Liber Quadratorum, 1225)、《花朵》(Flos, 1225)等,前者專論二次丟番圖方程,後者內容多為腓特烈二世(Frederick II)宮廷...
出現於克勞德·巴希特(英語:Claude Gaspard Bachet de Méziriac)的著作Problèmes plaisants et délectables的第二版在歐洲,輾轉相除法廣泛使用於丟番圖方程和連...
論文附有一個包括前20個通項值計算程式和結果的大表,每一行數據都對應著一個複雜的丟番圖方程。甚至早期彼得堡數學學派的一個缺點在這項研究中也有所反映,那就...
阿廷首先注意到,代數的理論可看成域中丟番圖方程的解的理論,即看到了在域K上可除代數的不存在性與一類方程具有K中多個未定元時的可解性之間的重要關係。曾炯...
