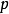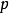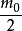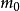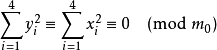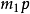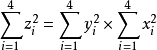基本介紹
發展簡史,驗證推導,
發展簡史
驗證推導
根據上面的四平方和恆等式及算術基本定理,可知只需證明質數可以表示成四個整數的平方和即可。
因 ,故只需證明奇質數可以表示成四個整數的平方和。
,故只需證明奇質數可以表示成四個整數的平方和。

根據引理一,奇質數 必有正倍數可以表示成四個整數的平方和。在這些倍數中,必存在一個最小的。設該數為
必有正倍數可以表示成四個整數的平方和。在這些倍數中,必存在一個最小的。設該數為 。又從引理一可知
。又從引理一可知 。
。



證明m0不會是偶數
設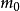 是偶數,且
是偶數,且 。由奇偶性可得知必有兩個數或四個數的奇偶性相同。不失一般性設
。由奇偶性可得知必有兩個數或四個數的奇偶性相同。不失一般性設 與
與 的奇偶性相同,
的奇偶性相同, 與
與 的奇偶性相同,則
的奇偶性相同,則 均為偶數,於是得到:
均為偶數,於是得到:
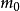










證明 m0 = 1
下面用反證法證明 。
。

設 。
。

與 矛盾。
矛盾。

引理一的證明
設 為奇素數,將和為
為奇素數,將和為 的剩餘兩個一組的分開,可得出
的剩餘兩個一組的分開,可得出 組,分別為
組,分別為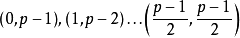 。
。



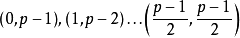
若 是模
是模 的二次剩餘,選取
的二次剩餘,選取 使得
使得 ,則
,則 ,定理得證。
,定理得證。