基本介紹
基本概念
構造引理法
概念
實例說明











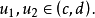




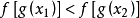










函式 | 單調狀況 | |||
內層函式 | 增 | 增 | 減 | 減 |
外層函式 | 增 | 減 | 增 | 減 |
複合函式 | 增 | 減 | 減 | 增 |












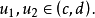




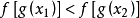










函式 | 單調狀況 | |||
內層函式 | 增 | 增 | 減 | 減 |
外層函式 | 增 | 減 | 增 | 減 |
複合函式 | 增 | 減 | 減 | 增 |
引理是為證明某個定理或解某個問題所要用到的命題。引理和定理沒有嚴格的區分,如果論證某個命題時,還沒有直接根據,需要某些還沒有被證明的結論,把它提出來加以...
亨澤爾引理(Hensel's Lemma )代數數論中的一個重要定理.由多項式在剩餘類域上的分解得出其在完備域上分解的定理.設域F,對非阿基米德賦值甲完備,O為賦值環,P為...
簡介《引理集》 阿基米德著作之一 只有阿拉伯文譯本傳下來,是15個初等幾何的問題集.也許不是阿基米德的原著而是後人收集整理的,因為在文章中不止一次提到阿基米德的...
莫爾斯引理(Morse lemma)是關於勢函式在非退化定態點附近定性性質的重要命題。...... 莫爾斯引理(Morse lemma)是關於勢函式在非退化定態點附近定性性質的重要命題。...
在有限群論,弗拉蒂尼引理指:若有限群G有正規子群H,H有西羅子群P,則G=NG(P)H,其中NG(P)是P的正規化子。...
里斯引理(Riesz lemma)揭示閉子空間與單位球面上某點的距離性質的重要引理。...... 里斯引理(Riesz lemma)揭示閉子空間與單位球面上某點的距離性質的重要引理。...
數學上,施瓦茲引理是複分析關於定義在單位開圓盤的全純函式的一個結果,以赫爾曼·阿曼杜斯·施瓦茨為名。...
約當(Jordan)引理,也翻譯作諾爾當引理,是複分析中的一條定理。...... 約當(Jordan)引理,也翻譯作諾爾當引理,是複分析中的一條定理。中文名 約當引理 外文名 ...
費馬(Fermat)引理是實分析中的一個定理,以皮埃爾·德·費馬命名。通過證明可導函式的每一個極值都是駐點(函式的導數在該點為零),該定理給出了一個求出可微...
佐恩引理(Zorn's Lemma)也被稱為庫拉托夫斯基-佐恩(Kuratowski-Zorn)引理,是集合論中一個重要的定理,其陳述為:在任何一非空的偏序集中,若任何鏈(即全序的子集...
伯恩賽德引理(Burnside's lemma),也叫伯恩賽德計數定理(Burnside's counting theorem),柯西-弗羅貝尼烏斯引理(Cauchy-Frobenius lemma)或軌道計數定理(orbit-counting ...
在測度論中,法圖引理說明了一個函式列的下極限的積分(在勒貝格意義上)和其積分的下極限的不等關係。法圖引理的名稱來源於法國數學家皮埃爾·法圖(Pierre Fatou),...
舒爾引理(<Schur lemma)描述不可約模之間同態的重要定理.該引理斷言:設P> > P:是群G的兩個不可約F表示,表示空間分別為Vi,Vz,。是叭到Y:的非零線性映射,...
高斯引理(Gauss lemma )多項式理論的主要命題之一即任意兩個本原多項式的乘積仍是一個本原多項式。 [1] 由高斯引理可知,任一非零的整係數多項式如果能夠分解為兩...
在隨機分析中,伊藤引理(Ito's lemma)是一條非常重要的性質。發現者為日本數學家伊藤清,他指出了對於一個隨機過程的函式作微分的規則。...
泵引理是形式語言與自動機理論中判定一個語言不是正則語言的重要工具,下面介紹的是其通用的形式,除此之外還有其推廣的強泵引理等。...
黎曼引理,是高等數學微積分領域的一條引理。...... 一元積分學中的黎曼引理: 若f(x)在[a,b]上可積, g(x)是以T為周期的函式,在[0,T]上可積;則成立:...
華氏引理(Hua's lemma)是得名自華羅庚的引理,是指數和的估計。...... 華氏引理(Hua's lemma)是得名自華羅庚的引理,是指數和的估計。華氏引理指出,若P是k次的...
圖基引理(Tukey's lemma)是選擇公理的一種等價形式,設有集合之集A,若任一集合A屬於該集A,若且唯若集合A的每個有窮子集都屬於該集A,則稱集A具有有窮特徵。...
多項式的高斯引理是數論和高等代數中的一條引理,是揭示本原多項式性質的結果。指出:多個本原多項式之乘積本原。...
在數論中,歐幾里得引理是根據歐幾里得的《幾何原本》第七卷的命題30推出的一個定理。這個引理說明:如果一個正整數整除另外兩個正整數的乘積,第一個整數與第二個...
西格爾引理(Siegel lemma)超越數理論的重要工具.利用著名的狄利克雷原則可以得到以下重要定理:設N為自然數集,Z表整數環,若mEN,n任N,nu=max 2,jm,a,E Z(1...
在數學中,九引理是一個對任意阿貝爾範疇(例如阿貝爾群範疇與模範疇)均成立的抽象結果,具體定義請參加正文。...
歐幾里得引理:若質數p|ab,則p|a或p|b。證明:若p|a則證明完畢。若否,p和a的最大公約數為1。根據裴蜀定理,存在整數對(m,n)使得ma+np=1。於是b=b(ma+...
許多非代數證明都用到了“增長引理”:當|z|足夠大時,首係數為1的n次多項式函式p(z)的表現如同z。一個更確切的表述是:存在某個正實數R,使得當|z| > R時...
