兩個本原多項式的乘積還是本原多項式。
基本介紹
- 中文名:高斯引理
- 提出者:高斯
- 套用學科:數學
- 適用領域範圍:代數學
引理
證明



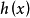
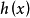



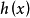







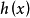








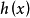
例子





兩個本原多項式的乘積還是本原多項式。



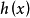
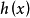



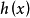







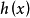








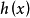




高斯引理(Gauss lemma )多項式理論的主要命題之一即任意兩個本原多項式的乘積仍是一個本原多項式。 [1] 由高斯引理可知,任一非零的整係數多項式如果能夠分解為兩...
高斯定理(Gauss' law)也稱為高斯通量理論(Gauss' flux theorem),或稱作散度定理、高斯散度定理、高斯-奧斯特羅格拉德斯基公式、奧氏定理或高-奧公式(通常...
多項式的高斯引理是數論和高等代數中的一條引理,是揭示本原多項式性質的結果。指出:多個本原多項式之乘積本原。...
高斯—馬爾可夫定理(Gauss–Markov theory)是指在給定經典線性回歸的假定下,最小二乘估計量是具有最小方差的線性無偏估計量的這一定理。高斯--馬爾可夫定理的意義...
高斯馬爾科夫定理是指在給定經典線性回歸模型的假定下,最小二乘估計量,在無偏線性估計一類中,有最小方差,就是說,它們是BLUE(best linear unbiased estimator)。...
高斯絕妙定理(Gauss theorem egregium),表達高斯曲率的一個定理。曲面的高斯曲率K可以用曲面的第一類基本量及它們的一階、二階偏導數來表示,因此,高斯曲率是曲面的...
高斯定律(Gauss' law):在靜電場中,穿過任一封閉曲面的電場強度通量只與封閉曲面內的電荷的代數和有關,且等於封閉曲面的電荷的代數和除以真空中的電容率。該定律...
引理是為證明某個定理或解某個問題所要用到的命題。引理和定理沒有嚴格的區分,如果論證某個命題時,還沒有直接根據,需要某些還沒有被證明的結論,把它提出來加以...
高斯判別準則,亦稱高斯引理,是判別二次剩餘的重要準則之一。...... 高斯判別準則,亦稱高斯引理,是判別二次剩餘的重要準則之一。高斯判別準則(Gauss criterion)亦稱高...
高斯-盧卡斯定理,又稱盧卡斯定理,該定理描述了復係數多項式的一個性質:多項式導數的根一定在原多項式的根所構成的凸包內。這一結論曾在1836被Carl Friedrich Gauss...
在微分幾何中,高斯-博內定理(亦稱高斯-博內公式)是關於曲面的圖形(由曲率表征)和拓撲(由歐拉示性數表征)間聯繫的一項重要表述。它是以卡爾·弗里德里希·高斯和...
高斯-奧斯特羅格拉茨基公式(Gauss-Ostro-gradsky formula)簡稱高一奧公式,亦稱散度定理、高斯公式、高斯散度定理,是指在向量分析中,一個把向量場通過曲面的流動(即...
有理根定理是高斯引理對多項式因式分解的特殊情況(單線性因子)。 如果導數係數 ,則整數根定理是有理根定理的特殊情況。 [1] 有理根定理套用 編輯 為了確定一個...
微分形式的庫侖定理也被稱為電場的高斯定律,是麥克斯韋方程組的一部分。 [4] 庫侖定律適用範圍 庫侖定律適用條件 在庫侖定律的常見表述中,通常會有真空和靜止,是...
