基本介紹
- 中文名:高斯馬爾科夫定理
- 外文名:best linear unbiased estimator
- 相關學科:統計學
- 條件:不相關性
高斯馬爾可夫定理
- 這裡最佳的意思是指相較於其他估計量有更小方差的估計量,同時把對估計量的尋找限制在所有可能的線性無偏估計量中。
- 值得注意的是這裡不需要假定誤差滿足獨立同分布(iid)或常態分配,而僅需要滿足零均值、不相關及同方差這三個稍弱的條件。
表述
簡單(一元)線性回歸模型[
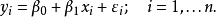
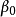
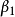
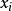
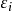

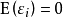
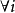
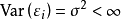
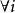
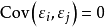
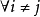
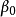
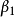
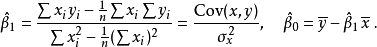
多元線性回歸模型
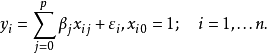
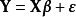
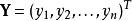
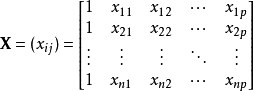
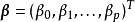
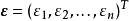
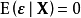

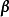

證明
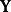
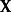
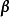

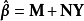
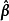
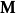
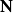
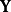
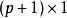
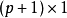

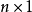


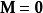
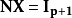

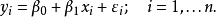
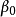
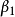
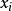
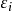

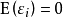
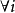
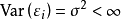
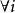
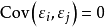
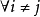
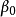
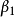
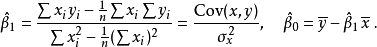
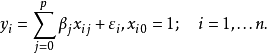
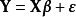
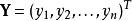
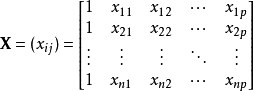
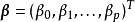
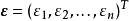
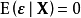

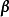

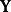
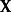
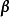

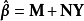
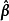
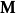
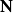
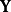
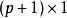
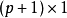

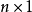


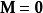
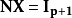
高斯馬爾科夫定理是指在給定經典線性回歸模型的假定下,最小二乘估計量,在無偏線性估計一類中,有最小方差,就是說,它們是BLUE(best linear unbiased estimator)。...
高斯—馬爾可夫定理高斯-馬爾科夫定理的具體內容 編輯 高斯-馬爾可夫定理總共分為對OLS(Ordinary least square)普通線性方程有5個假設。...
1.5.1 LS估計量的性質1.5.2 高斯—馬爾科夫定理1.5.3 推斷程式1.5.4 數值例子(續1.4.5節中的例子)1.6 兩變數回歸模型的方差分析1.7 雙變數回歸模型中的預測...
高斯-馬爾科夫定理在給定經典線性回歸模型的假定下,最小二乘估計量,在無偏線性估計量一類中,有最小方差,即它們滿足最優線性無偏性。...
根據高斯——馬爾科夫定理,多重相關性並不影響最小二乘估計量的無偏性和最小方差性。但是,雖然最小二乘估計量在所有線性無偏估計量中是方差最小的,但是這個...
在建立一般的線性回歸模型時,當數據總體滿足高斯—馬爾科夫定理,由最小二乘法有式中: B 為估計的變數;Y ={ }為因變數;X ={ 為自變數,當自變數之間存在嚴重...
§2.6 OLS估計的統計性質:高斯-馬爾科夫定理40 §2.7 判定係數R2:“擬合優度”的一個度量42 §2.8 回歸係數的估計與假設檢驗47 §2.9 簡單線性回歸模型的預測...
第四節 高斯—馬爾科夫定理再探 第六章 正態條件下回歸的推論 第一節 問題的引入 第二節 問題的預解決 第三節 派生的內容:自由度 第四節 回歸係數...
6.3.3高斯 馬爾科夫定理6.3.4多元線性回歸模型的擬合優度6.3.5多元線性回歸模型的顯著性檢驗6.3.6SPSS 20的多元線性回歸分析思考與練習...
