基本介紹
定義


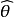


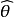
量化特性
誤差
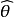


均方誤差
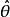

一致性




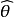


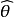
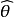


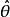


在統計學中,估計量是基於觀測數據計算一個已知量的估計值的法則:於是估計量(estimator)、被估量(estimand)和估計值(estimate)是有區別的。估計量用來估計未知總體...
對於待估參數,不同的樣本值就會得到不同的估計值。這樣,要確定一個估計量的好壞,就不能僅僅依據某次抽樣的結果來衡量,而必須由大量抽樣的結果來衡量。對此,一個...
估計量的無縮性和最小方差性,是優良估計量的兩個可要標誌。因此,稱最小方差無偏估計為最優估計。然而,由於樣本的隨機性,任何估計量的方差也不能任意地小。...
回歸估計量是指回歸估計方法中所用到的調查變數以及與該變數有線性關係的輔助變數。...
比率估計量可以是指為估計總體比率所建立的估計量,也可以是指通過總體總值、均值同總體比率之間的關係去估計總體總值、均值所建立的估計量。...
參數估計(parameter estimation),統計推斷的一種。根據從總體中抽取的隨機樣本來估計總體分布中未知參數的過程。從估計形式看,區分為點估計與區間估計:從構造估計量的...
在數理統計中,一般用子樣觀測值求出的統計量來估計總體*的一個未知參數,此統計量稱為參數的估計量。子樣一組觀測值所對應估計量的值,稱為參數的估計值。尋求...
漸近無偏估計量(asymptotic unbiased estimator)是指當樣本容量n 無限增大時,近似無偏的估計量。...
估計誤差,是指數據處理過程中對誤差的估計,有多種統計表示方式。在統計學中,估計誤差是此估計量的期望值與估計參數的真值之差。誤差為零的估計量或決策規則稱為...
統計估計(statistical estimation)是統計推斷的一種形式,統計估計的方法是用樣本的函式來估計總體的分布函式、分布參數或數字特徵。例如,用樣本均值估計總體均值;用經驗...
最佳無偏估計量(值)best unbiased estimator多個不同的無偏估計量中方差最小的無偏枯計量。 ...
無偏估計是用樣本統計量來估計總體參數時的一種無偏推斷。估計量的數學期望等於被估計參數的真實值,則稱此估計量為被估計參數的無偏估計,即具有無偏性,是一種...
估計理論是對收信端接收到的混有噪聲的信號,用統計學方法估計出信號的參量或狀態的理論。估計分為參量估計和狀態估計兩類。參量和狀態的區別是:前者隨著時間保持不...
一致估計亦稱相合估計和相容估計,是一種優良點估計。按收斂的意義不同將一致估計分為兩種:弱一致估計和強一致估計。點估計又稱定值估計,是指直接用樣本平均數或...
參量估計(parameter estimation )用統計學中的估計理論,對接收端收到的混有噪聲和干擾的信號樣本,估計出有用信號參量(如振幅、頻率、相位、到達時間等)的方法。...
霍維茨-湯普森估計量是由霍維茨和湯普森作出關於不等機率不放回抽樣,樣本容量為n時對總體均值或總體總值的一個估計量。...
如果一個參數的估計量具有線性(估計量是樣本觀察值的線性函式)、無偏(估計量的數學期望等於真值)和估計誤差方差最小等統計學性質,稱其為最佳線性無偏估計量。 應...
卡普蘭一梅爾估計量(Kaplan-Meier estimator )一種估計量.當壽命數據為不完全樣本時,一種估計未知總體生存函式的非參數估計量...
若g(θ)的無偏估計量T0(X1,X2,...,Xn)對g(θ)的任意無偏估計量T(X1,X2,...,Xn)都有Var[T0]≤Var[T],則稱T0為g(θ)的一致最小方差無偏估計...
兩個無偏估計量的方差之比值,是比較兩個估計量方差大小的數字特徵。 ...... 兩個無偏估計量的方差之比值,是比較兩個估計量方差大小的數字特徵。 [1] ...
最小均方誤差估計量(minimum mean squareerror estimation)一種參數估計量.是使均方誤差達到最小的估計量.設T(X)是參數B的估計量,對B的任一估計量T*(X),...
