在微分幾何中,高斯-博內定理(亦稱高斯-博內公式)是關於曲面的圖形(由曲率表征)和拓撲(由歐拉示性數表征)間聯繫的一項重要表述。它是以卡爾·弗里德里希·高斯和皮埃爾·奧西安·博內命名的,前者發現了定理的一個版本但從未發表,後者1848年發表了該定理的一個特例。
基本介紹
- 中文名:高斯-博內定理
- 外文名:Gauss–Bonnet theorem
- 領域:數學
定理內容
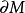
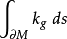
一般化的高斯-博內定理
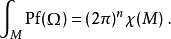
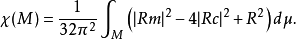
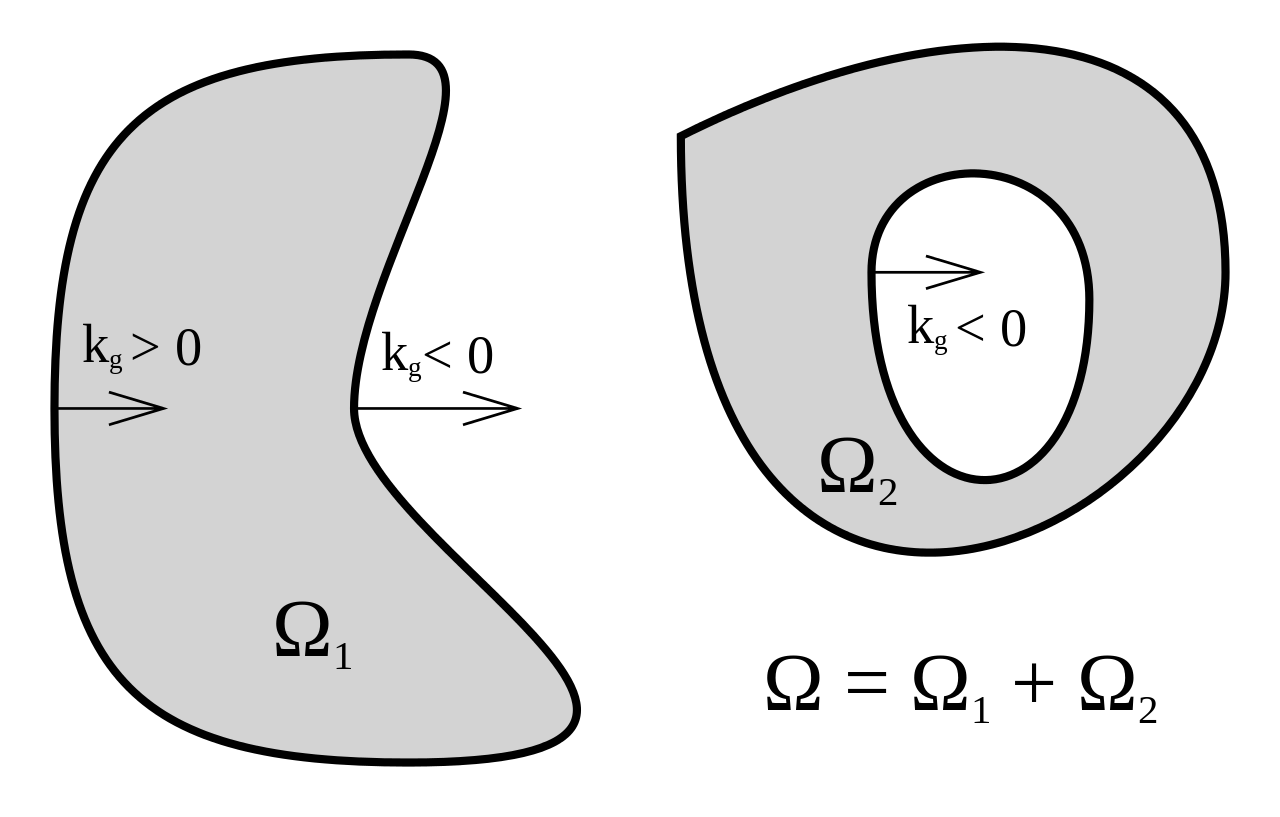
在微分幾何中,高斯-博內定理(亦稱高斯-博內公式)是關於曲面的圖形(由曲率表征)和拓撲(由歐拉示性數表征)間聯繫的一項重要表述。它是以卡爾·弗里德里希·高斯和皮埃爾·奧西安·博內命名的,前者發現了定理的一個版本但從未發表,後者1848年發表了該定理的一個特例。
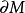
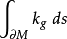
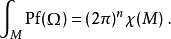
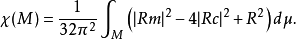
在微分幾何中,高斯-博內定理(亦稱高斯-博內公式)是關於曲面的圖形(由曲率表征)和拓撲(由歐拉示性數表征)間聯繫的一項重要表述。它是以卡爾·弗里德里希·高斯和...
高斯—馬爾可夫定理(Gauss–Markov theory)是指在給定經典線性回歸的假定下,最小二乘估計量是具有最小方差的線性無偏估計量的這一定理。高斯--馬爾可夫定理的意義...
高斯-盧卡斯定理,又稱盧卡斯定理,該定理描述了復係數多項式的一個性質:多項式導數的根一定在原多項式的根所構成的凸包內。這一結論曾在1836被Carl Friedrich Gauss...
高斯曲率2.高斯-博內定理 高斯-博內定理將曲面的總曲率和它的歐拉示性數聯繫起來,並且給出了一個局部幾何性質和全局拓撲性質的重要關聯。...
[2] [5] 幾何和拓撲學中的許多大定理,包括黎曼-羅赫定理(Riemann-Roch Theorem)、希茲布魯赫符號差定理(Hirzebruch's Signature Theorem)、高斯-博內-陳定理(Gaus...
高斯-博內定理將曲面的全曲率和曲面的拓撲性質聯繫起來:高斯映射推廣 編輯 高斯映射可以定義在Rn中的超曲面上,從超曲面映射到Rn中的單位球面Sn-1。...
曲面的整體性質的一個重要結果是高斯-博內定理,它指明,在閉曲面S上,總曲率K的積除以2π就是曲面的歐拉等於1減去曲面上洞的個數,是個拓撲不變數,因而這個定理...
對於閉黎曼曲面,歐拉示性數也可以通過曲率的積分得到—參看對於二維情況的高斯-博內定理(Gauss-Bonnet)和對於一般情況的廣義高斯-博內定理。高斯-博內定理的離散情況...
這是整體微分幾何的奠基性的工作。隨後,中國數學家陳省身從外微分的觀點出發,推廣了曲面上的高斯-博內定理。從此微分幾何成為現代數學不可缺少的領域。 [1] ...
其中轉數是單位切向量關於起點的繞數, 或者等價的高斯映射的次數. 局部不變數曲率和整體拓撲不變數指數的關係是高維黎曼幾何的代表性結果,如高斯-博內定理。 [1]...
這一相位是勢能面交叉點的奇異性與高斯-博內定理的結果。即使在絕熱過程中,貝瑞相位仍有一定的動力學效應,可以觀測到振動光譜中能級的下移。...
套用黎曼 - 赫爾維茨公式和高斯 - 博內定理,可以計算 的屬。 對於素數級≥5,其中 是歐拉特徵, 是組PSL(2,p)的順序, 是球(2,3,p)的角。 這產生一個...
早在40年代,陳省身他結合微分幾何與拓撲學的方法,完成了兩項劃時代的重要工作:高斯-博內-陳定理和Hermitian流形的示性類理論,為大範圍微分幾何提供了不可缺少的...
在黎曼球面的情況,高斯-博內定理表明常曲率度量必須有正的曲率K。因而該度量必須通過球極投影等度於中半徑為的球面。對於黎曼球面上的ζ-圖,K = 1度量可以給出...
其真空期望值的指數確定耦合常數g,為緊湊的世界面通過高斯-博內定理和歐拉示性數χ = 2 − 2g作為∫R = 2πχ,其中g是對手柄數進行計數的屬性,因此由特定...
這個理論由陳省身和安德烈·韋伊於1940年代建立,是發展示性類理論的重要步驟。這個結果推廣了陳-高斯-博內定理。中文名 陳-韋伊同態 外文名 Chern–Weil ...
在黎曼球面的情況,高斯-博內定理表明常曲率度量必須有正的曲率K。因而該度量必須通過球極投影等度於R3中半徑為1/√K的球面。對於黎曼球面上的ζ-圖,K = 1度量...
(1)證明了著名的高斯-博內-陳省身定理、陳省身-萊雪夫定理和威爾默定理的統一定理,發現了幾何量、分析量、拓撲量之間新的內在聯繫,並套用該定理獲得了曲率與拓撲...
此即高斯-博內(Gauss-Bonnet)定理,是更一般的阿蒂亞-辛格(Atiyah-Singer)指標定理的特例[1] 。歐拉類陳(省身)類 陳(省身)類(Chern class)是復向量叢的一種...
